
ЁОЬтФПЁПаЁеХОгЊФГвЛЯћЗбЦЗзЈТєЕъЃЌвбжЊИУЯћЗбЦЗЕФНјМлЮЊУПМў40дЊЃЌИУЕъУПдТЯњЪлСПЃЈАйМўЃЉгыЯњЪлЕЅМлxЃЈдЊ/МўЃЉжЎМфЕФЙиЯЕгУЯТЭМЕФвЛелЯпБэЪОЃЌжАЙЄУПШЫУПдТЙЄзЪЮЊ1000дЊЃЌИУЕъЛЙгІНЛИЖЕФЦфЫќЗбгУЮЊУПдТ10000дЊ.

ЃЈ1ЃЉАбyБэЪОЮЊxЕФКЏЪ§ЃЛ
ЃЈ2ЃЉЕБЯњЪлМлЮЊУПМў50дЊЪБЃЌИУЕъе§КУЪежЇЦНКтЃЈМДРћШѓЮЊСуЃЉЃЌЧѓИУЕъЕФжАЙЄШЫЪ§ЃЛ
ЃЈ3ЃЉШєИУЕъжЛга20УћжАЙЄЃЌЮЪЯњЪлЕЅМлЖЈЮЊЖрЩйдЊЪБЃЌИУзЈТєЕъПЩЛёЕУзюДѓдТРћШѓЃПЃЈзЂЃКРћШѓ=ЪеШы-жЇГіЃЉ
ЁОД№АИЁПЃЈ1ЃЉ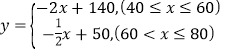 ЃЈ2ЃЉ30УћдБЙЄЃЈ3ЃЉЯњЪлЕЅМлЖЈЮЊ55Лђ70дЊЪБЃЌИУзЈТєЕъдТРћШѓзюДѓ
ЃЈ2ЃЉ30УћдБЙЄЃЈ3ЃЉЯњЪлЕЅМлЖЈЮЊ55Лђ70дЊЪБЃЌИУзЈТєЕъдТРћШѓзюДѓ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЗжБ№ЧѓГіЕБ![]() КЭ
КЭ![]() ЪБЕФНтЮіЪНЃЌНјЖјПЩЕУЫљЧѓНсЙћЃЛЃЈ2ЃЉЩшИУЕъгажАЙЄmУћЃЌИљОнЬтвтЕУЕНЙигкmЕФЗНГЬЃЌЧѓНтПЩЕУЫљЧѓЃЛЃЈ3ЃЉгЩЬтвтЕУЕНРћШѓЕФКЏЪ§ЙиЯЕЪНЃЌИљОнЗжЖЮКЏЪ§зюжЕЕФЧѓЗЈПЩЕУЫљЧѓЃЎ
ЪБЕФНтЮіЪНЃЌНјЖјПЩЕУЫљЧѓНсЙћЃЛЃЈ2ЃЉЩшИУЕъгажАЙЄmУћЃЌИљОнЬтвтЕУЕНЙигкmЕФЗНГЬЃЌЧѓНтПЩЕУЫљЧѓЃЛЃЈ3ЃЉгЩЬтвтЕУЕНРћШѓЕФКЏЪ§ЙиЯЕЪНЃЌИљОнЗжЖЮКЏЪ§зюжЕЕФЧѓЗЈПЩЕУЫљЧѓЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЩш
ЪБЃЌЩш![]() ЃЌ
ЃЌ
гЩЬтвтЕУЕу![]() дкКЏЪ§ЕФЭМЯѓЩЯЃЌ
дкКЏЪ§ЕФЭМЯѓЩЯЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
ЭЌРэЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
ЁрЫљЧѓЙиЯЕЪНЮЊ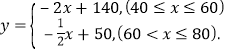
ЃЈ2ЃЉЩшИУЕъгажАЙЄmУћЃЌ
ЕБx=50ЪБЃЌИУЕъЕФзмЪеШыЮЊ![]() дЊЃЌ
дЊЃЌ
гжИУЕъЕФзмжЇГіЮЊ1000m+10000дЊЃЌ
вРЬтвтЕУ40000=1000m+10000,
НтЕУЃКm=30.
ЫљвдДЫЪБИУЕъга30УћдБЙЄЃЎ
ЃЈ3ЃЉШєИУЕъжЛга20УћжАЙЄЃЌ
дђдТРћШѓ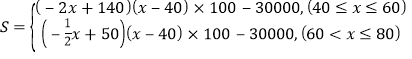
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ыљвдx=55ЪБЃЌSШЁзюДѓжЕ15000дЊЃЛ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
Ыљвдx=70ЪБЃЌSШЁзюДѓжЕ15000дЊЃЛ
ЙЪЕБx=55Лђx=70ЪБЃЌSШЁзюДѓжЕ15000дЊЃЌ
МДЯњЪлЕЅМлЖЈЮЊ55Лђ70дЊЪБЃЌИУзЈТєЕъдТРћШѓзюДѓЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ= ![]() sinx+cosІиxЃЈІиЃО0ЃЉЕФЭМЯѓгыxжсНЛЕуЕФКсзјБъвРДЮЙЙГЩвЛИіЙЋВюЮЊ
sinx+cosІиxЃЈІиЃО0ЃЉЕФЭМЯѓгыxжсНЛЕуЕФКсзјБъвРДЮЙЙГЩвЛИіЙЋВюЮЊ ![]() ЕФЕШВюЪ§СаЃЌАбКЏЪ§fЃЈxЃЉЕФЭМЯѓбиxжсЯђзѓЦНвЦ
ЕФЕШВюЪ§СаЃЌАбКЏЪ§fЃЈxЃЉЕФЭМЯѓбиxжсЯђзѓЦНвЦ ![]() ИіЕЅЮЛЃЌЕУЕНКЏЪ§gЃЈxЃЉЕФЭМЯѓЃЌдђЃЈ ЃЉ
ИіЕЅЮЛЃЌЕУЕНКЏЪ§gЃЈxЃЉЕФЭМЯѓЃЌдђЃЈ ЃЉ
A.gЃЈxЃЉЪЧЦцКЏЪ§
B.gЃЈxЃЉЙигкжБЯпx=Љ ![]() ЖдГЦ
ЖдГЦ
C.gЃЈxЃЉдк[ ![]() ЃЌ
ЃЌ ![]() ]ЩЯЪЧдіКЏЪ§
]ЩЯЪЧдіКЏЪ§
D.ЕБxЁЪ[ ![]() ЃЌ
ЃЌ ![]() ]ЪБЃЌgЃЈxЃЉЕФжЕгђЪЧ[2ЃЌ1]
]ЪБЃЌgЃЈxЃЉЕФжЕгђЪЧ[2ЃЌ1]
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=3mxЉ ![]() ЉЃЈ3+mЃЉlnxЃЌШєЖдШЮвтЕФmЁЪЃЈ4ЃЌ5ЃЉЃЌx1 ЃЌ x2ЁЪ[1ЃЌ3]ЃЌКугаЃЈaЉln3ЃЉmЉ3ln3ЃО|fЃЈx1ЃЉЉfЃЈx2ЃЉ|ГЩСЂЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ЉЃЈ3+mЃЉlnxЃЌШєЖдШЮвтЕФmЁЪЃЈ4ЃЌ5ЃЉЃЌx1 ЃЌ x2ЁЪ[1ЃЌ3]ЃЌКугаЃЈaЉln3ЃЉmЉ3ln3ЃО|fЃЈx1ЃЉЉfЃЈx2ЃЉ|ГЩСЂЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦЗХЦОЯњЩЬдквЛЙуГЁЫцЛњВЩЗУФаадКЭХЎадгУЛЇИї50УћЃЌЦфжаУПЬьЭцЮЂаХГЌЙ§6аЁЪБЕФгУЛЇСаЮЊЁАЮЂаХПиЁБЃЌЗёдђГЦЦфЮЊЁАЗЧЮЂаХПиЁБЃЌЕїВщНсЙћШчЯТЃК
ЮЂаХПи | ЗЧЮЂаХПи | КЯМЦ | |
Фаад | 26 | 24 | 50 |
ХЎад | 30 | 20 | 50 |
КЯМЦ | 56 | 44 | 100 |
ЃЈ1ЃЉИљОнвдЩЯЪ§ОнЃЌФмЗёга95%ЕФАбЮеШЯЮЊЁАЮЂаХПиЁБгыЁАадБ№ЁБгаЙиЃП
ЃЈ2ЃЉЯжДгЕїВщЕФХЎадгУЛЇжаАДЗжВуГщбљЕФЗНЗЈбЁГі5ШЫЃЌЧѓЫљГщШЁЕФ5ШЫжаЁАЮЂаХПиЁБКЭЁАЗЧЮЂаХПиЁБЕФШЫЪ§ЃЛ
ЃЈ3ЃЉДгЃЈ2ЃЉжаГщШЁЕФ5ЮЛХЎаджаЃЌдйЫцЛњГщШЁ3ШЫдљЫЭРёЦЗЃЌЪдЧѓГщШЁ3ШЫжаЧЁга2ШЫЮЛЁАЮЂаХПиЁБЕФИХТЪ.
ВЮПМЙЋЪН:  ЃЌЦфжа
ЃЌЦфжа![]() .
.
ВЮПМЪ§ОнЃК
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаУќЬтЃКЂйКЏЪ§![]() дк
дк![]() ЩЯЕФжЕгђЮЊ
ЩЯЕФжЕгђЮЊ![]() ЃЛЂкКЏЪ§
ЃЛЂкКЏЪ§![]() ЪЧЦцКЏЪ§ЃЛЂлКЏЪ§
ЪЧЦцКЏЪ§ЃЛЂлКЏЪ§![]() дк
дк![]() ЩЯЪЧМѕКЏЪ§ЃЛЦфжае§ШЗЕФИіЪ§ЮЊ______ЃЎ
ЩЯЪЧМѕКЏЪ§ЃЛЦфжае§ШЗЕФИіЪ§ЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ2МўДЮЦЗКЭ3Мўе§ЦЗЛьЗХдквЛЦ№ЃЌЯжашвЊЭЈЙ§МьВтНЋЦфЧјЗжЃЌУПДЮЫцЛњМьВтвЛМўВњЦЗЃЌМьВтКѓВЛЗХЛиЃЌжБЕНМьВтГі2МўДЮЦЗЛђепМьВтГі3Мўе§ЦЗЪБМьВтНсЪј.
ЃЈ1ЃЉЧѓзюКѓШЁГіЕФЪЧе§ЦЗЕФИХТЪЃЛ
ЃЈ2ЃЉвбжЊУПМьВтвЛМўВњЦЗашвЊЗбгУ100дЊЃЌЩш![]() БэЪОжБЕНМьВтГі2МўДЮЦЗЛђепМьВтГі3Мўе§ЦЗЪБЫљашвЊЕФМьВтЗбгУ(ЕЅЮЛЃКдЊ)ЃЌЧѓ
БэЪОжБЕНМьВтГі2МўДЮЦЗЛђепМьВтГі3Мўе§ЦЗЪБЫљашвЊЕФМьВтЗбгУ(ЕЅЮЛЃКдЊ)ЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ
ЕФЗжВМСаКЭЪ§бЇЦкЭћ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() ЕФЖЈвхгђЮЊAЃЌШє
ЕФЖЈвхгђЮЊAЃЌШє![]() ЪБзмга
ЪБзмга![]() ЮЊЕЅКЏЪ§.Р§ШчЃЌКЏЪ§
ЮЊЕЅКЏЪ§.Р§ШчЃЌКЏЪ§![]() =2x+1ЃЈ
=2x+1ЃЈ![]() ЃЉЪЧЕЅКЏЪ§.ЯТСаУќЬтЃК
ЃЉЪЧЕЅКЏЪ§.ЯТСаУќЬтЃК
ЂйКЏЪ§![]() =
=![]() ЃЈx
ЃЈx![]() RЃЉЪЧЕЅКЏЪ§ЃЛЂкШє
RЃЉЪЧЕЅКЏЪ§ЃЛЂкШє![]() ЮЊЕЅКЏЪ§ЃЌ
ЮЊЕЅКЏЪ§ЃЌ![]() Чв
Чв![]() дђ
дђ![]() ЃЛЂлШєfЃКA
ЃЛЂлШєfЃКA![]() BЮЊЕЅКЏЪ§ЃЌдђЖдгкШЮвтb
BЮЊЕЅКЏЪ§ЃЌдђЖдгкШЮвтb![]() BЃЌЫќжСЖргавЛИідЯѓЃЛ
BЃЌЫќжСЖргавЛИідЯѓЃЛ
ЂмКЏЪ§fЃЈxЃЉдкФГЧјМфЩЯОпгаЕЅЕїадЃЌдђfЃЈxЃЉвЛЖЈЪЧЕЅКЏЪ§.ЦфжаЕФецУќЬтЪЧ .ЃЈаДГіЫљгаецУќЬтЕФБрКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкФГГЌЪаЃЌЫцЛњЕїВщСЫ100УћЙЫПЭЙКЮяЪБЪЙгУЪжЛњжЇИЖжЇИЖЕФЧщПіЃЌЕУЕНШчЯТЕФ![]() СаСЊБэЃЌвбжЊДгЦфжаЪЙгУЪжЛњжЇИЖЕФШЫШКжаЫцЛњГщШЁ1ШЫЃЌГщЕНЧрФъЕФИХТЪЮЊ
СаСЊБэЃЌвбжЊДгЦфжаЪЙгУЪжЛњжЇИЖЕФШЫШКжаЫцЛњГщШЁ1ШЫЃЌГщЕНЧрФъЕФИХТЪЮЊ![]() .
.
ЃЈ1ЃЉИљОнвбжЊЬѕМўЭъГЩ![]() СаСЊБэЃЌВЂИљОнДЫзЪСЯХаЖЯЪЧЗёга99.9%ЕФАбЮеШЯЮЊЁАГЌЪаЙКЮягУЪжЛњжЇИЖгыФъСфгаЙиЁБ.
СаСЊБэЃЌВЂИљОнДЫзЪСЯХаЖЯЪЧЗёга99.9%ЕФАбЮеШЯЮЊЁАГЌЪаЙКЮягУЪжЛњжЇИЖгыФъСфгаЙиЁБ.
ЃЈ2)ЯжАДееЁАЪЙгУЪжЛњжЇИЖЁБКЭЁАВЛЪЙгУЪжЛњжЇИЖЁБНјааЗжВуГщбљЃЌДгет100УћЙЫПЭжаГщШЁШнСПЮЊ5ЕФбљБОЃЌЧѓЁАДгбљБОжаШЮбЁ3ШЫЃЌдђ3ШЫжажСЩй2ШЫЪЙгУЪжЛњжЇИЖЁБЕФИХТЪ.
ЧрФъ | жаРЯФъ | КЯМЦ | |
ЪЙгУЪжЛњжЇИЖ | 60 | ||
ВЛЪЙгУЪжЛњжЇИЖ | 28 | ||
КЯМЦ | 100 |
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ИНЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшaЃЌbЁЪRЃЌcЁЪ[0ЃЌ2ІаЃЉЃЌШєЖдШЮвтЪЕЪ§xЖМга2sinЃЈ3xЉ ![]() ЃЉ=asinЃЈbx+cЃЉЃЌЖЈвхдкЧјМф[0ЃЌ3Іа]ЩЯЕФКЏЪ§y=sin2xЕФЭМЯѓгыy=cosxЕФЭМЯѓЕФНЛЕуИіЪ§ЪЧdИіЃЌдђТњзуЬѕМўЕФгаађЪЕЪ§зщЃЈaЃЌbЃЌcЃЌdЃЉЕФзщЪ§ЮЊЃЈ ЃЉ
ЃЉ=asinЃЈbx+cЃЉЃЌЖЈвхдкЧјМф[0ЃЌ3Іа]ЩЯЕФКЏЪ§y=sin2xЕФЭМЯѓгыy=cosxЕФЭМЯѓЕФНЛЕуИіЪ§ЪЧdИіЃЌдђТњзуЬѕМўЕФгаађЪЕЪ§зщЃЈaЃЌbЃЌcЃЌdЃЉЕФзщЪ§ЮЊЃЈ ЃЉ
A.7
B.11
C.14
D.28
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com