
【题目】已知函数![]() (a为实常数).
(a为实常数).
(1)若![]() ,作函数
,作函数![]() 的图象并写出单调减区间;
的图象并写出单调减区间;
(2)当![]() 时,设
时,设![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)当![]() 时对于函数
时对于函数![]() 和函数
和函数![]() ,若对任意的
,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数m的值.
成立,求实数m的值.
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震释放出的能量![]() (单位:焦耳)与地震里氏震级
(单位:焦耳)与地震里氏震级![]() 之间的关系为
之间的关系为![]() .
.
(1)已知地震等级划分为里氏![]() 级,根据等级范围又分为三种类型,其中小于
级,根据等级范围又分为三种类型,其中小于![]() 级的为“小地震”,介于
级的为“小地震”,介于![]() 级到
级到![]() 级之间的为“有感地震”,大于
级之间的为“有感地震”,大于![]() 级的为“破坏性地震”若某次地震释放能量约
级的为“破坏性地震”若某次地震释放能量约![]() 焦耳,试确定该次地震的类型;
焦耳,试确定该次地震的类型;
(2)2008年汶川地震为里氏![]() 级,2011年日本地震为里氏
级,2011年日本地震为里氏![]() 级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取
级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小电子产品2018年的价格为9元/件,年销量为![]() 件,经销商计划在2019年将该电子产品的价格降为
件,经销商计划在2019年将该电子产品的价格降为![]() 元/件(其中
元/件(其中![]() ),经调查,顾客的期望价格为5元/件,经测算,该电子产品的价格下降后年销量新增加了
),经调查,顾客的期望价格为5元/件,经测算,该电子产品的价格下降后年销量新增加了![]() 件(其中常数
件(其中常数![]() ).已知该电子产品的成本价格为4元/件.
).已知该电子产品的成本价格为4元/件.
(1)写出该电子产品价格下降后,经销商的年收益![]() 与实际价格
与实际价格![]() 的函数关系式:(年收益=年销售收入-成本)
的函数关系式:(年收益=年销售收入-成本)
(2)设![]() ,当实际价格最低定为多少时,仍然可以保证经销商2019年的收益比2018年至少增长20%?
,当实际价格最低定为多少时,仍然可以保证经销商2019年的收益比2018年至少增长20%?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=![]() x+4,动圆⊙O:x2+y2=r2(1<r<2),菱形ABCD的一个内角为60°,顶点A、B在直线l上,顶点C、D在⊙O上.当r变化时,求菱形ABCD的面积S的取值范围.
x+4,动圆⊙O:x2+y2=r2(1<r<2),菱形ABCD的一个内角为60°,顶点A、B在直线l上,顶点C、D在⊙O上.当r变化时,求菱形ABCD的面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某辆汽车以![]() 千米
千米![]() 小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() 时,每小时的油耗(所需要的汽油量)为
时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以120千米![]() 小时的速度行驶时,每小时的油耗为11.5升,欲使每小时的油耗不超过9升,求
小时的速度行驶时,每小时的油耗为11.5升,欲使每小时的油耗不超过9升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶100千米的油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类似于平面直角坐标系,定义平面斜坐标系:设数轴![]() 、
、![]() 的交点为
的交点为![]() ,与
,与![]() 、
、![]() 轴正方向同向的单位向量分别是
轴正方向同向的单位向量分别是![]() 、
、![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,其中
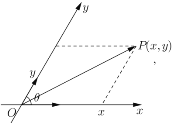
,其中![]() ,由平面向量基本定理:对于平面内的向量
,由平面向量基本定理:对于平面内的向量![]() ,存在唯一有序实数对
,存在唯一有序实数对![]() ,使得
,使得![]() ,把
,把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标,也叫做向量
中的坐标,也叫做向量![]() 在斜坐标系
在斜坐标系![]() 中的坐标,记为
中的坐标,记为![]() ,在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如
,在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如![]() 时,方程
时,方程![]() 表示斜坐标系内一条过点
表示斜坐标系内一条过点![]() ,且方向向量为
,且方向向量为![]() 的直线.
的直线.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
(2)若![]() ,已知点
,已知点![]() 和直线
和直线![]() ;
;
①求![]() 的一个法向量;
的一个法向量;
②求点![]() 到直线
到直线![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com