
【题目】已知![]() 菱形
菱形![]() 所在平面,
所在平面,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,得
,得![]() ,由线面平行的判定定理得
,由线面平行的判定定理得![]() 平面
平面![]() ,连接
,连接![]() 交
交![]() 与点
与点![]() ,连接
,连接![]() ,得
,得![]() ,进而得
,进而得![]() 平面
平面![]() ,再由面面平行的判定,得平面
,再由面面平行的判定,得平面![]() 平面
平面![]() ,进而得到
,进而得到![]() 平面
平面![]() .
.
(2)建立空间直角坐标系![]() ,求解平面
,求解平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
详解:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]()
∵![]() 为
为![]() 的中点,
的中点,
∴![]()
∴![]() 平面
平面![]() .……………………2分
.……………………2分
连接![]() 交
交![]() 与点
与点![]() ,连接
,连接![]()
∵![]() 为
为![]() 的中点,
的中点,
∴![]()
∴![]() 平面
平面![]() ……………………4分
……………………4分
∵![]()
∴平面![]() 平面
平面![]()
又![]()
![]() 平面
平面![]()
∴![]() 平面
平面![]() .…………6分
.…………6分
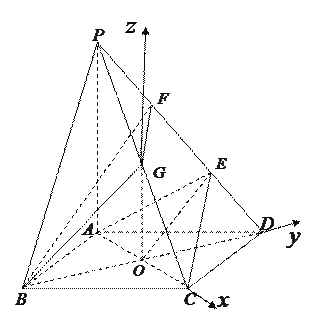
(2)如图,建立空间直角坐标系![]()
则![]()
![]()
![]()
∴![]() ………7分
………7分
设平面![]() 的法向量为
的法向量为![]()
则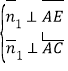 ,
,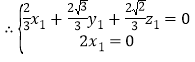 即
即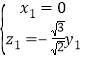
不放设![]() 得
得![]() ……………………8分
……………………8分
设平面![]() 的法向量为
的法向量为![]()
则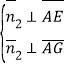 ,
,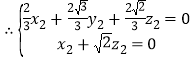 即
即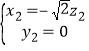
不放设![]() 得
得![]() ……………………10分
……………………10分
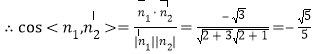
则二面角![]() 的余弦值为
的余弦值为![]() ……………………12分
……………………12分


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣lnx+a﹣1,g(x)= ![]() +ax﹣xlnx,其中a>0.
+ax﹣xlnx,其中a>0.
(1)求f(x)的单调区间;
(2)当x≥1时,g(x)的最小值大于 ![]() ﹣lna,求a的取值范围.
﹣lna,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几个孩子在一棵枯树上玩耍,他们均不慎失足下落.已知
(![]() )甲在下落的过程中依次撞击到树枝
)甲在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )乙在下落的过程中依次撞击到树枝
)乙在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )丙在下落的过程中依次撞击到树枝
)丙在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )丁在下落的过程中依次撞击到树枝
)丁在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )戊在下落的过程中依次撞击到树枝
)戊在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() .
.
倒霉和李华在下落的过程中撞到了从![]() 到
到![]() 的所有树枝,根据以上信息,在李华下落的过程中,和这
的所有树枝,根据以上信息,在李华下落的过程中,和这![]() 根树枝不同的撞击次序有( )种.
根树枝不同的撞击次序有( )种.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E. 
(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年高校自主招生期间,某校把学生的平时成绩按“百分制”折算,选出前![]() 名学生,并对这
名学生,并对这![]() 名学生按成绩分组,第一组
名学生按成绩分组,第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() .如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
.如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.

(1)请写出第一、二、三、五组的人数,并在图中补全频率分布直方图;
(2)若![]() 大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
①若![]() 大学本次面试中有
大学本次面试中有![]() ,
,![]() ,
,![]() 三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为
三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为![]() ,
,![]() ,
,![]() ,求甲同学面试成功的概率;
,求甲同学面试成功的概率;
②若![]() 大学决定在这6名学生中随机抽取3名学生接受考官
大学决定在这6名学生中随机抽取3名学生接受考官![]() 的面试,第3组有
的面试,第3组有![]() 名学生被考官
名学生被考官![]() 面试,求
面试,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线 ![]() =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com