练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知$sinα=-\frac{{\sqrt{5}}}{5}$，α为第四象限角，求$\frac{cosα+sinα}{cosα-sinα}$的值．

    分析 利用同角三角函数的基本关系，求得cosα tanα的值，可得 $\frac{cosα+sinα}{cosα-sinα}$=$\frac{1+tanα}{1-tanα}$ 的值．

    解答 解：∵已知$sinα=-\frac{{\sqrt{5}}}{5}$，α为第四象限角，∴cosα=$\sqrt{{1-sin}^{2}α}$=$\frac{2\sqrt{5}}{5}$，$tanα=-\frac{1}{2}$，
    ∴$\frac{cosα+sinα}{cosα-sinα}$=$\frac{1+tanα}{1-tanα}$=$\frac{1}{3}$．

    点评 本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

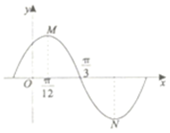    6．若函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象如图所示，M，N分别是这段图象的最高点与最低点，且OM⊥ON，则A=（　　）
    A．$\frac{π}{6}$B．$\frac{\sqrt{7}π}{12}$C．$\frac{\sqrt{7}π}{6}$D．$\frac{\sqrt{7}π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知圆M：x2+y2-2x+ay=0（a＞0）被x轴和y轴截得的弦长相等，则圆M被直线x+y=0截得的弦长为（　　）
    A．4B．$\sqrt{2}$C．2$\sqrt{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知关于x的函数f（x）=x2-2$\sqrt{b}x+{a^2}$，若点（a，b）是区域$\left\{\begin{array}{l}x+y-6≤0\\ x＞0\\ y＞0\end{array}$内的随机点，则函数f（x）在R上有零点的概率为（　　）
    A．$\frac{2}{3}$B．$\frac{11}{27}$C．$\frac{1}{3}$D．$\frac{5}{27}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在△ABC中，若$|{\overrightarrow{AB}+\overrightarrow{AC}}|=|{\overrightarrow{AB}-\overrightarrow{AC}}|$，则△ABC的形状是（　　）
    A．等腰三角形B．直角三角形C．等边三角形D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

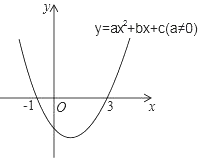    8．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法：①2a+b=0；②当-1≤x≤3时，y＜0；③若（x1，y1）、（x2，y2）在函数图象上，当x1＜x2时，y1＜y2；④9a+3b+c=0其中正确的是（　　）
    A．①②④B．①④C．①②③D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知椭圆的方程为：$\frac{x^2}{4}+\frac{y^2}{3}=1$，点P的坐标为$（1，\frac{3}{2}）$，一条不过点P直线l：y=kx+b交椭圆于A，B，PA⊥PB，且AB被y轴平分，则直线l的方程为y=$±\frac{3}{2}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知log32=a，log27=b，则log37等于（　　）
    A．a+bB．a-bC．abD．$\frac{a}{b}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知抛物线y2=2x，点P为抛物线上任意一点，P在y轴上的射影为Q，点M（2，3），则PQ与PM的长度之和的最小值为$\frac{3\sqrt{5}-1}{2}$．

    查看答案和解析>>

    同步练习册答案