
 件(n∈N*).
件(n∈N*). ,可知数列{sn}不成等差也不成等比数列,但是两者的差
,可知数列{sn}不成等差也不成等比数列,但是两者的差  构成等比数列,对于这类问题一般有以下两种方法求解:
构成等比数列,对于这类问题一般有以下两种方法求解: +
+ +
+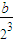 +…+
+…+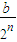 =b(2-
=b(2- )
)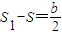 ,
,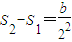 ,…
,… ,累加结合等比数列的求和公式可求Sn
,累加结合等比数列的求和公式可求Sn ),设获利为Tn,则有Tn=s•10-1000n=40000(2-
),设获利为Tn,则有Tn=s•10-1000n=40000(2- )-1000n,
)-1000n,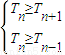 ,代入结合n为正整数解不等式可求n,进而可求S的最大值
,代入结合n为正整数解不等式可求n,进而可求S的最大值 +
+ +
+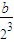 +…+
+…+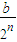 =b(2-
=b(2- )(广告费为1千元时,s=b+
)(广告费为1千元时,s=b+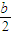 ;2千元时,s=b+
;2千元时,s=b+ +
+ ;…n千元时s=b+
;…n千元时s=b+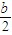 +
+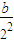 +
+ +…+
+…+ )
) ,相加得Sn-S=
,相加得Sn-S=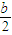 +
+ +
+ +…+
+…+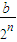 ,
, +
+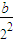 +
+ +…+
+…+ =b(2-
=b(2- ).
). ),设获利为t,则有t=s•10-1000n=40000(2-
),设获利为t,则有t=s•10-1000n=40000(2- )-1000n
)-1000n ,得
,得 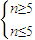 ,故n=5,此时s=7875.
,故n=5,此时s=7875.

科目:高中数学 来源: 题型:
| x2 | y3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 n |
查看答案和解析>>
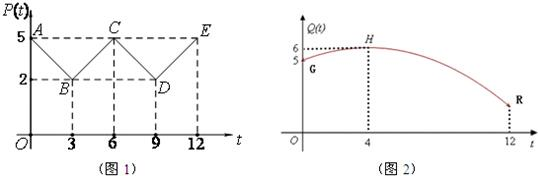
科目:高中数学 来源:2011年江苏省高考数学预测试卷及最后一讲(解析版) 题型:解答题
 ),试列出P(x,y)所满足的条件,并求出相应的最大值.
),试列出P(x,y)所满足的条件,并求出相应的最大值.
查看答案和解析>>
科目:高中数学 来源:2011年江苏省无锡市滨湖区高考数学模拟试卷(解析版) 题型:解答题
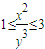 ),试列出P(x,y)所满足的条件,并求出相应的最大值.
),试列出P(x,y)所满足的条件,并求出相应的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com