已知矩阵
A=

,若点P(1,1)在矩阵
A对应的变换作用下得到点P′(0,-8).
(1)求实数a的值;
(2)求矩阵
A的特征值.
(1)由

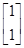
=
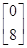
,得a+1=-8,所以a=-9.
(2)由(1)知
A=
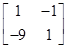
,则矩阵
A的特征多项式为f(λ)=
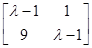
=(λ-1)
2-9=λ
2-2λ-8,令f(λ)=0,所以矩阵
A的特征值为-2或4.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知二阶矩阵M有特征值

及对应的一个特征向量

,并且矩阵M对应的变换将点

变换成

,求矩阵M。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知矩阵
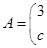
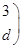
,若矩阵
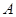
属于特征值6的一个特征向量为
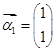
,属于特征值1的一个特征向量
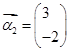
.
(1)求矩阵
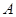
的逆矩阵;
(2)计算
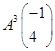
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
如果复数z=cosθ+isinθ,θ∈(0,
),记n(n∈N
*)个Z的积为Z
N,通过验证n=2,n=3,n=4…,的结果z
n,推测z
n=______.(结果用θ,n,i表示)
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
在直角坐标平面内,将每个点绕原点按逆时针方向旋转

的变换

所对应的矩阵为

,将每个点横、纵坐标分别变为原来的

倍的变换

所对应的矩阵为

.
(1)求矩阵

的逆矩阵

;
(2)求曲线

先在变换

作用下,然后在变换

作用下得到的曲线方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
二阶矩阵
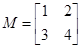
;
(1)求点
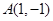
在变换M作用下得到的点
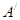
;
(2)设直线
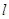
在变换M作用下得到了直线
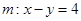
,求
的方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
矩阵
M=
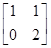
有特征向量为
e1=
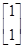
,
e2=
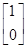
,
(1)求
e1和
e2对应的特征值;
(2)对向量
α=
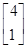
,记作
α=
e1+3
e2,利用这一表达式间接计算
M4α,
M10α.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知矩阵
M=

,若矩阵
M的逆矩阵
M-1=

,求a、b的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
求直线x+y=5在矩阵
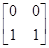
对应的变换作用下得到的图形.
查看答案和解析>>

 ,若点P(1,1)在矩阵A对应的变换作用下得到点P′(0,-8).
,若点P(1,1)在矩阵A对应的变换作用下得到点P′(0,-8). 的变换
的变换 所对应的矩阵为
所对应的矩阵为 ,将每个点横、纵坐标分别变为原来的
,将每个点横、纵坐标分别变为原来的 倍的变换
倍的变换 所对应的矩阵为
所对应的矩阵为 .
. 的逆矩阵
的逆矩阵 ;
; 先在变换
先在变换 作用下,然后在变换
作用下,然后在变换 作用下得到的曲线方程.
作用下得到的曲线方程.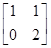 有特征向量为e1=
有特征向量为e1=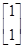 ,e2=
,e2=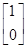 ,
,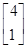 ,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.
,记作α=e1+3e2,利用这一表达式间接计算M4α,M10α.