练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

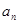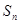    （本小题12分）设等差数列{}的前项和为，已知＝，．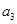

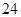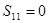    (1) 求数列{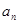}的通项公式； （2）当n为何值时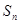，最大，并求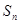的最大值．

     

    【答案】

    （1）.（2）当或时，最大，且的最大值为120.

    【解析】(1)由＝，可建立关于a1和d的方程，求出a1和d的值，从而确定{}的通项公式.

    （2）在（1）的基础上，可求出,从而利用二次函数的性质可求出其最大值，要注意n取正整数.

    （1）依题意有，解之得，∴.

    （2）由（1）知，＝40，，

    ∴ ＝＝＝－4＋121，

    故当或时，最大，且的最大值为120.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （08年全国卷Ⅰ文）（本小题满分12分）

    四棱锥中，底面为矩形，侧面底面，，，．

    （Ⅰ）证明：；

    （Ⅱ）设侧面为等边三角形，求二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省四地六校联考高三上学期第二次月考文科数学卷 题型：解答题

    （本小题满分12分）

    某小区要建一座八边形的休闲小区，它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域，计划在正方形MNPQ上建一座“观景花坛”，造价为4 200元/m2，在四个相同的矩形上（图中阴影部分）铺花岗岩地坪，造价为210元/m2，再在四个空角（如△DQH等）上铺草坪，造价为80元/m2.

    （1）设总造价为S元，AD长为m，试建立S与x的函数关系；

    （2）当x为何值时，S最小？并求这个最小值.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年内蒙古包头市高三上学期期中考试数学试卷 题型：解答题

    （本小题满分12分）

    已知{an}是各项均为正数的等比例数列，且

    （Ⅰ）求{an}的通项公式；

    （Ⅱ）设，求数列{bn}的前N项和Tn。

     

    查看答案和解析>>

    科目：高中数学 来源：山东省枣庄市2010届高三年级调研考试数学（文科）试题 题型：解答题

    （本小题满分12分）

       袋内装有6个球，每个球上都记有从1到6的一个号码，设号码为n的球重克，这些球等可能地从袋里取出（不受重量、号码的影响）。

       （1）如果任意取出1球，求其重量大于号码数的概率；

       （2）如果不放回地任意取出2球，求它们重量相等的概率。

     

    查看答案和解析>>

    科目：高中数学 来源：2010年孝感高中高一下学期期末考试数学卷 题型：解答题

    （本小题满分12分）

           设棋子在正四面体ABCD的表面从一个顶点移向另外三个顶点是等可能的，现投掷骰子根据其点数决定棋子是否移动：若投出的点数是偶数，棋子移动到另一个顶点；若投出的点数是奇数，则棋子不动.若棋子的初始位置在顶点A.

    求：（Ⅰ）投了2次骰子，棋子才到达顶点B的概率；

    （Ⅱ）记投了n次骰子，棋子在顶点B的概率为.求.

     

    查看答案和解析>>

    同步练习册答案