
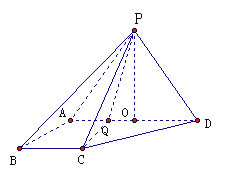
【题目】如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,O为AD中点.
,O为AD中点.

(1)求证:PO⊥平面ABCD;
(2)求直线BD与平面PAB所成角的正弦值;
(3)线段AD上是否存在点![]() ,使得它到平面PCD的距离为
,使得它到平面PCD的距离为![]() .
.
【答案】(1)见解析.
(2) ![]() .
.
(3)见解析.
【解析】
(1)先证明PO⊥AD,再证明PO⊥平面ABCD.(2)先证明∠DBP为直线BD与平面PAB所成角,再求直线BD与平面PAB所成角的正弦值.(3) 假设存在点Q,设QD=x,再求出x的值.
(1)证明:在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD,平面![]() 平面ABCD=AD,
平面ABCD=AD, ![]() 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
(2)由(1)PO⊥平面ABCD,![]() ,又AB⊥AD,
,又AB⊥AD,![]()
![]() ,
,
![]() .
. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 为直线BD与平面PAB所成的角.
为直线BD与平面PAB所成的角.
在Rt△DPB中,![]() ,
,![]() ,
,![]() ,
,
所以直线BD与平面PAB所成角的正弦值为![]() .
.
(3)假设存在点Q,使得它到平面PCD的距离为![]() .
.
设QD=x,则![]() ,由(Ⅱ)得CD=OB=
,由(Ⅱ)得CD=OB=![]() ,
,
在Rt△POC中, ![]()
所以PC=CD=DP![]() ,
,![]()
由VP-DQC=VQ-PCD 得![]() ,
,![]() ,
,
所以存在点Q满足题意,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】解答题。
(1)已知 ![]() 是奇函数,求常数m的值;
是奇函数,求常数m的值;
(2)画出函数y=|3x﹣1|的图象,并利用图象回答:k为何值时,方程|3x﹣1|=k无解?有一解?有两解?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=cos ![]() x,对任意的实数t,记f(x)在[t,t+1]上的最大值为M(t),最小值为m(t),则函数h(t)=M(t)﹣m(t)的值域为 .
x,对任意的实数t,记f(x)在[t,t+1]上的最大值为M(t),最小值为m(t),则函数h(t)=M(t)﹣m(t)的值域为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线![]() 的两个焦点坐标是
的两个焦点坐标是![]() ,且离心率为
,且离心率为![]() ;
;
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 表示曲线
表示曲线![]() 的
的![]() 轴左边部分,若直线
轴左边部分,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的取值范围;
的取值范围;
(3)在条件(2)下,如果![]() ,且曲线
,且曲线![]() 上存在点
上存在点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足P= ![]() (其中0≤x≤a,a为正常数).已知生产该产品还需投入成本6(P+
(其中0≤x≤a,a为正常数).已知生产该产品还需投入成本6(P+ ![]() )万元(不含促销费用),产品的销售价格定为(4+
)万元(不含促销费用),产品的销售价格定为(4+ ![]() )元/件.
)元/件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com