
ΓΨΧβΡΩΓΩ‘ΎΡ≥¥Έ≤β ‘ΚσΘ§“ΜΈΜάœ Π¥”±ΨΑύ48Ά§―ß÷–ΥφΜζ≥ι»Γ6ΈΜΆ§―ßΘ§ΥϊΟ«ΒΡ”οΈΡΓΔάζ Ζ≥…Φ®»γœ¬±μΘΚ
―ß…ζ±ύΚ≈ | 1 | 2 | 3 | 4 | 5 | 6 |
”οΈΡ≥…Φ® | 60 | 70 | 74 | 90 | 94 | 110 |
άζ Ζ≥…Φ® | 58 | 63 | 75 | 79 | 81 | 88 |
(1)»τΙφΕ®”οΈΡ≥…Φ®≤ΜΒΆ”Ύ90Ζ÷ΈΣ”≈–ψΘ§άζ Ζ≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΈΣ”≈–ψΘ§“‘ΤΒ¬ ΉςΗ≈¬ Θ§Ζ÷±πΙάΦΤΗΟΑύ”οΈΡΓΔάζ Ζ≥…Φ®”≈–ψΒΡ»Υ ΐΘΜ
(2)”Ο…œ±μ ΐΨίΜ≠≥ω…ΔΒψΆΦ“ΉΖΔœ÷άζ Ζ≥…Φ®![]() ”κ”οΈΡ≥…Φ®
”κ”οΈΡ≥…Φ®![]() ΨΏ”–Ϋœ«ΩΒΡœΏ–‘œύΙΊΙΊœΒΘ§«σ
ΨΏ”–Ϋœ«ΩΒΡœΏ–‘œύΙΊΙΊœΒΘ§«σ![]() ”κ
”κ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ®œΒ ΐΨΪ»ΖΒΫ0.1Θ©.
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ®œΒ ΐΨΪ»ΖΒΫ0.1Θ©.
≤ΈΩΦΙΪ ΫΘΚΜΊΙι÷±œΏΖΫ≥Χ «![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ§
Θ§ ![]()
ΓΨ¥πΑΗΓΩΘ®1Θ©”οΈΡΓΔάζ Ζ≥…Φ®”≈–ψΒΡ»Υ ΐΖ÷±πΈΣ24ΓΔ16ΘΜΘ®2Θ©![]() .
.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”…±μ÷– ΐΨίΒΟ≥ω”οΈΡΓΔάζ Ζ≥…Φ®ΈΣ”≈–ψΒΡΤΒ¬ Θ§¥”Εχ«σ≥ωΗΟΑύ”οΈΡΓΔάζ Ζ≥…Φ®”≈–ψΒΡ»Υ ΐΘΜΘ®2Θ©”…±μ÷– ΐΨίΦΤΥψ![]() Θ§«σ≥ωΜΊΙιœΒ ΐΘ§–¥≥ωœΏ–‘ΜΊΙιΖΫ≥Χ.
Θ§«σ≥ωΜΊΙιœΒ ΐΘ§–¥≥ωœΏ–‘ΜΊΙιΖΫ≥Χ.
‘ΧβΫβΈωΘ®1Θ©”…±μ÷– ΐΨίΘ§”οΈΡ≥…Φ®ΓΔάζ Ζ≥…Φ®ΈΣ”≈–ψΒΡΤΒ¬ Ζ÷±πΈΣ![]()
Ι ΗΟΑύ”οΈΡΓΔάζ Ζ≥…Φ®”≈–ψΒΡ»Υ ΐΖ÷±πΈΣ24ΓΔ16
Θ®2Θ©”…±μ÷– ΐΨίΩ…ΒΟΘ§ ![]()
![]() Θ§
Θ§ ![]()
Υυ“‘Θ§ 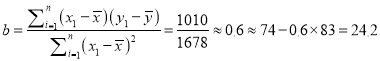
Υυ“‘![]() ”κ
”κ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ«σΨ≠Ιΐ»ΐΒψAΘ®1Θ§4Θ©Θ§BΘ®©¹2Θ§3Θ©Θ§CΘ®4Θ§©¹5Θ©ΒΡ‘≤ΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() Θ®
Θ®![]() Θ©Θ§»τΆ÷‘≤
Θ©Θ§»τΆ÷‘≤![]() …œΒΡ“ΜΕ·ΒψΒΫ”“ΫΙΒψΒΡΉνΕΧΨύάκΈΣ
…œΒΡ“ΜΕ·ΒψΒΫ”“ΫΙΒψΒΡΉνΕΧΨύάκΈΣ![]() Θ§«“”“ΫΙΒψΒΫ÷±œΏ
Θ§«“”“ΫΙΒψΒΫ÷±œΏ![]() ΒΡΨύάκΒ»”ΎΕΧΑκ÷αΒΡ≥ΛΘ§“―÷Σ
ΒΡΨύάκΒ»”ΎΕΧΑκ÷αΒΡ≥ΛΘ§“―÷Σ![]() Θ§Ιΐ
Θ§Ιΐ![]() ΒΡ÷±œΏ”κΆ÷‘≤ΫΜ”Ύ
ΒΡ÷±œΏ”κΆ÷‘≤ΫΜ”Ύ![]() ΝΫΒψ.
ΝΫΒψ.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΥψΖ®ΒΡ≥Χ–ρΆΦ»γΆΦΥυ ΨΘ§Τδ÷– δ»κΒΡ±δΝΩx‘Ύ1Θ§2Θ§3Θ§Γ≠Θ§30’β30Ηω’ϊ ΐ÷–Β»Ω…ΡήΥφΜζ≤ζ…ζΘ° 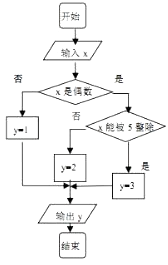
Θ®1Θ©Ζ÷±π«σ≥ωΑ¥≥Χ–ρΩρΆΦ’ΐ»Ζ±ύ≥Χ‘Υ–– ± δ≥ωyΒΡ÷ΒΈΣiΒΡΗ≈¬ PiΘ®i=1Θ§2Θ§3Θ©ΘΜ
Θ®2Θ©ΦΉΓΔ““ΝΫΆ§―ß“άΨίΉ‘ΦΚΕ‘≥Χ–ρΩρΆΦΒΡάμΫβΘ§ΗςΉ‘±ύ–¥≥Χ–ρ÷ΊΗ¥‘Υ––n¥ΈΚσΘ§Ά≥ΦΤΦ«¬ΦΝΥ δ≥ωyΒΡ÷ΒΈΣiΘ®i=1Θ§2Θ§3Θ©ΒΡΤΒ ΐΘ§œ¬Οφ «ΦΉΓΔ““ΥυΉςΤΒ ΐΆ≥ΦΤ±μΒΡ≤ΩΖ÷ ΐΨίΘΚ ΦΉΒΡΤΒ ΐΆ≥ΦΤ±μΘ®≤ΩΖ÷Θ©
‘Υ––¥Έ ΐ | δ≥ωy=1ΒΡΤΒ ΐ | δ≥ωy=2ΒΡΤΒ ΐ | δ≥ωy=3ΒΡΤΒ ΐ |
50 | 24 | 19 | 7 |
Γ≠ | Γ≠ | Γ≠ | Γ≠ |
2000 | 1027 | 776 | 197 |
““ΒΡΤΒ ΐΆ≥ΦΤ±μΘ®≤ΩΖ÷Θ©
‘Υ––¥Έ ΐ | δ≥ωy=1ΒΡΤΒ ΐ | δ≥ωy=2ΒΡΤΒ ΐ | δ≥ωy=3ΒΡΤΒ ΐ |
50 | 26 | 11 | 13 |
Γ≠ | Γ≠ | Γ≠ | Γ≠ |
2000 | 1051 | 396 | 553 |
Β±n=2000 ±Θ§ΗυΨί±μ÷–ΒΡ ΐΨίΘ§Ζ÷±π–¥≥ωΦΉΓΔ““Υυ±ύ≥Χ–ρΗςΉ‘ δ≥ωyΒΡ÷ΒΈΣiΘ®i=1Θ§2Θ§3Θ©ΒΡΤΒ¬ Θ®”ΟΖ÷ ΐ±μ ΨΘ©Θ§≤Δ≈–ΕœΦΉΓΔ““÷–Υ≠Υυ±ύ–¥ΒΡ≥Χ–ρΖϊΚœΥψΖ®“Σ«σΒΡΩ…Ρή–‘Ϋœ¥σΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψ![]() ΈΣ‘≤
ΈΣ‘≤![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() «‘≤…œΒΡΕ·ΒψΘ§œΏΕΈ
«‘≤…œΒΡΕ·ΒψΘ§œΏΕΈ![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ
ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ![]() ”ΎΒψ
”ΎΒψ![]() .
.
Θ®1Θ©«σΒψ![]() ΒΡΙλΦΘ
ΒΡΙλΦΘ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η![]() Θ§
Θ§ ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ®“λ”ΎΒψ
Θ®“λ”ΎΒψ![]() Θ©Θ§ΙΐΒψ
Θ©Θ§ΙΐΒψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κ
”κ![]() «ψ–±Ϋ«ΜΞ≤Ι.
«ψ–±Ϋ«ΜΞ≤Ι.
ΔΌ÷±œΏ![]() ΒΡ–±¬ «ΖώΈΣΕ®÷ΒΘΩ»τ «Θ§«σ≥ωΗΟΕ®÷ΒΘΜ»τ≤Μ «Θ§ΥΒΟςάμ”…ΘΜ
ΒΡ–±¬ «ΖώΈΣΕ®÷ΒΘΩ»τ «Θ§«σ≥ωΗΟΕ®÷ΒΘΜ»τ≤Μ «Θ§ΥΒΟςάμ”…ΘΜ
ΔΎ…η![]() ”κ
”κ![]() ΒΡΟφΜΐ÷°ΚΆΈΣ
ΒΡΟφΜΐ÷°ΚΆΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
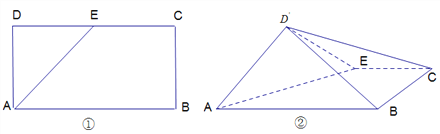
ΓΨΧβΡΩΓΩ»γΆΦΔΌΘ§‘ΎΨΊ–Έ![]() ÷–Θ§
÷–Θ§ ![]() Θ§
Θ§ ![]() «
«![]() ΒΡ÷–ΒψΘ§ΫΪ»ΐΫ«–Έ
ΒΡ÷–ΒψΘ§ΫΪ»ΐΫ«–Έ![]() ―Ί
―Ί![]() Ζ≠’έΒΫΆΦΔΎΒΡΈΜ÷ΟΘ§ ΙΒΟΤΫΟφ
Ζ≠’έΒΫΆΦΔΎΒΡΈΜ÷ΟΘ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() .
.
(Δώ)‘ΎœΏΕΈ![]() …œ»ΖΕ®Βψ
…œ»ΖΕ®Βψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§≤Δ÷ΛΟςΘΜ
Θ§≤Δ÷ΛΟςΘΜ
(Δρ)«σ![]() ”κ
”κ![]() Υυ‘ΎΤΫΟφΙΙ≥…ΒΡ»ώΕΰΟφΫ«ΒΡ’ΐ«–÷Β.
Υυ‘ΎΤΫΟφΙΙ≥…ΒΡ»ώΕΰΟφΫ«ΒΡ’ΐ«–÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒ»≤ν ΐΝ–{an}ΒΡ«ΑnœνΚΆSn Θ§ »τa3+a7©¹a10=8Θ§a11©¹a4=4Θ§‘ρS13Β»”ΎΘ® Θ©
A.152
B.154
C.156
D.158
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘Ρ≥–ΘΗΏ“ΜΡξΦΕ―ß…ζ≤ΈΦ”…γ«χΖΰΈώ¥Έ ΐΫχ––Ά≥ΦΤΘ§ΥφΜζ≥ι»Γ![]() Οϊ―ß…ζΉςΈΣ―υ±ΨΘ§ΒΟΒΫ’β
Οϊ―ß…ζΉςΈΣ―υ±ΨΘ§ΒΟΒΫ’β![]() Οϊ―ß…ζ≤ΈΦ”…γ«χΖΰΈώΒΡ¥Έ ΐ.ΗυΨί¥Υ ΐΨίΉς≥ωΝΥΤΒ ΐ”κΤΒ¬ ΒΡΆ≥ΦΤ±μΚΆΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γœ¬ΘΚ
Οϊ―ß…ζ≤ΈΦ”…γ«χΖΰΈώΒΡ¥Έ ΐ.ΗυΨί¥Υ ΐΨίΉς≥ωΝΥΤΒ ΐ”κΤΒ¬ ΒΡΆ≥ΦΤ±μΚΆΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ»γœ¬ΘΚ
Ζ÷Ήι | ΤΒ ΐ | ΤΒ¬ |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
ΚœΦΤ |
| 1 |

Θ®1Θ©«σ≥ω±μ÷–![]() ΦΑΆΦ÷–
ΦΑΆΦ÷–![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ© ‘ΙάΦΤΥϊΟ«≤ΈΦ”…γ«χΖΰΈώΒΡΤΫΨυ¥Έ ΐΘΜ
Θ®3Θ©‘ΎΥυ»Γ―υ±Ψ÷–Θ§¥”≤ΈΦ”…γ«χΖΰΈώΒΡ¥Έ ΐ≤Μ…Ό”Ύ20¥ΈΒΡ―ß…ζ÷–»Έ―Γ2»ΥΘ§«σ÷Ν…Ό1»Υ≤ΈΦ”…γ«χΖΰΈώ¥Έ ΐ‘Ύ«χΦδ![]() ΡΎΒΡΗ≈¬ .
ΡΎΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
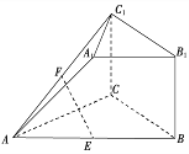
ΓΨΧβΡΩΓΩ‘Ύ»γΆΦΥυ ΨΒΡΦΗΚΈΧε÷–Θ§ΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘ§
«ΨΊ–ΈΘ§ ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() ΓΈ
ΓΈ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Ζ÷±π «
Ζ÷±π «![]() Θ§
Θ§ ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°
Θ®ΔώΘ©«σ÷ΛΘΚ ![]() ΓΈΤΫΟφ
ΓΈΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©«σ÷ΛΘΚ ![]() ΤΫΟφ
ΤΫΟφ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com