
【题目】已知函数f(x)=x2+|x|﹣|x﹣5|+2.
(1)求不等式f(x)<0的解集;
(2)若关于x的不等式|f(x)|≤m的整数解仅有11个,求m的取值范围.
【答案】
(1)解:当x≤0时,f(x)=x2﹣x+x﹣5+2=x2﹣3,
由x2﹣3<0解得﹣ ![]() <x<
<x< ![]() ,取﹣
,取﹣ ![]() <x≤0;
<x≤0;
当0<x<5时,f(x)=x2+x+x﹣5+2=x2+2x﹣3,
由x2+2x﹣3<0解得﹣3<x<1,取0<x<1;
当x≥5时,f(x)=x2+x﹣x+5+2=x2+7,
由x2+7<0无解;
综上,不等式f(x)<0的解集为(﹣ ![]() ,1)
,1)
(2)解:由(1)知,f(x)=  ,
,
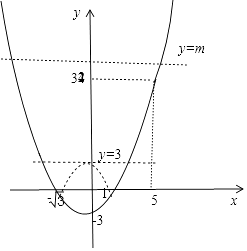
画出f(x)的图象如图所示;
若关于x的不等式|f(x)|≤m的整数解仅有11个,
当m=32时,由x2+7≤32,解得x≤5;
由x2﹣3≤32,解得﹣ ![]() ≤x,
≤x,
满足不等式|f(x)|≤m的整数解仅有11个;
当m=33时,由x2+7≤33,解得x≤ ![]() ;
;
由x2﹣3≤33,解得﹣6≤x,
满足不等式|f(x)|≤m的整数解仅有12个;
不满足题意;
当m=31时,由x2+7≤31,解得x≤ ![]() ;
;
由x2﹣3≤31,解得﹣ ![]() ≤x,
≤x,
满足不等式|f(x)|≤m的整数解仅有10个;
不满足题意;
综上,m的取值范围是[32,33).
【解析】(1)讨论x的取值,去掉绝对值,化简f(x),求出不等式f(x)<0的解集;(2)由(1)写出f(x)解析式,画出f(x)的图象,结合图象,求出不等式|f(x)|≤m的整数解仅有11个时,求出m的取值范围.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】函数![]() 在同一个周期内,当
在同一个周期内,当![]() 时y取最大值1,当
时y取最大值1,当![]() 时,y取最小值﹣1.
时,y取最小值﹣1.
(1)求函数的解析式y=f(x);
(2)函数y=sinx的图象经过怎样的变换可得到y=f(x)的图象?
(3)若函数f(x)满足方程f(x)=a(0<a<1),求在[0,2π]内的所有实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f( ![]() )=﹣
)=﹣ ![]() x3+
x3+ ![]() x2﹣m,g(x)=﹣
x2﹣m,g(x)=﹣ ![]() x3+mx2+(a+1)x+2xcosx﹣m.
x3+mx2+(a+1)x+2xcosx﹣m.
(1)若曲线y=f(x)仅在两个不同的点A(x1 , f(x1)),B(x1 , f(x2))处的切线都经过点(2,t),求证:t=3m﹣8,或t=﹣ ![]() m3+
m3+ ![]() m2﹣m.
m2﹣m.
(2)当x∈[0,1]时,若f(x)≥g(x)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数既是奇函数,又在[﹣1,1]上单调递增是( )
A.f(x)=|sinx|
B.f(x)=ln ![]()
C.f(x)= ![]() (ex﹣e﹣x)
(ex﹣e﹣x)
D.f(x)=ln( ![]() ﹣x)
﹣x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆与双曲线有相同的焦点![]() ,
,![]() ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为![]() ,直线
,直线![]() 与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为
与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1﹣BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题: ①MB∥平面A1DE;
②存在某个位置,使DE⊥A1C;
③存在某个位置,使A1D⊥CE;
④点A1在半径为 ![]() 的圆面上运动,
的圆面上运动,
其中正确的命题个数是( )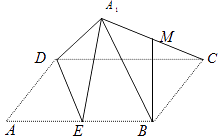
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com