已知函数f(x)=x2+(a+1)x+lg|a+2|(a∈R,且a≠-2)
(I)若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和,求g(x)和h(x)的解析式;
(II)命题P:函数f(x)在区间[(a+1)2,+∞)上是增函数;命题Q:函数g(x)是减函数.如果命题P、Q有且仅有一个是真命题,求a的取值范围;
(III)在(II)的条件下,比较f(2)与3-lg2的大小.
【答案】
分析:(I)设f(x)=g(x)+h(x),利用函数的奇偶性,组成方程组,即可求得函数的解析式;
(II)将函数f(x)配方,利用函数在区间[(a+1)
2,+∞)上是增函数,可得命题P为真的条件;利用函数g(x)=(a+1)x是减函数,可得命题Q为真的条件,从而可求命题P、Q有且仅有一个是真命题,a的取值范围;
(III)由(I)得f(2)=2a+lg|a+2|+6,确定函数v(a)=2a+lg(a+2)+6,在区间
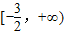
上为增函数,即可求得结论.
解答:解:(I)∵f(x)=g(x)+h(x),g(-x)=-g(x),h(-x)=h(x)
∴f(-x)=-g(x)+h(x)
∴
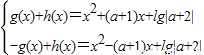
解得g(x)=(a+1)x,h(x)=x
2+lg|a+2|;
(II)∵函数f(x)=x
2+(a+1)x+lg|a+2|=
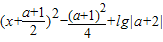
在区间[(a+1)
2,+∞)上是增函数,
∴
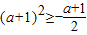
,解得a≥-1或a≤-

且a≠-2
又由函数g(x)=(a+1)x是减函数,得a+1<0,∴a<-1且a≠-2
∴命题P为真的条件是:a≥-1或a≤-

且a≠-2,命题Q为真的条件是:a<-1且a≠-2.
又∵命题P、Q有且仅有一个是真命题,
∴
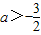
(III)由(I)得f(2)=2a+lg|a+2|+6
∵
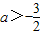
,∴f(2)=2a+lg(a+2)+6
设函数v(a)=2a+lg(a+2)+6,v′(a)=2+
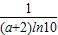
>0.
∴函数v(a)在区间
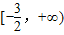
上为增函数.
又∵
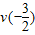
=3-lg2,∴当
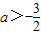
时,v(a)>
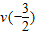
,即f(2)>3-lg2.
点评:本题考查函数单调性与奇偶性的结合,考查函数的单调性,考查大小比较,正确运用函数的单调性是关键.

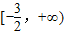 上为增函数,即可求得结论.
上为增函数,即可求得结论.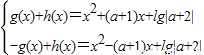
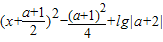 在区间[(a+1)2,+∞)上是增函数,
在区间[(a+1)2,+∞)上是增函数,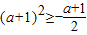 ,解得a≥-1或a≤-
,解得a≥-1或a≤- 且a≠-2
且a≠-2 且a≠-2,命题Q为真的条件是:a<-1且a≠-2.
且a≠-2,命题Q为真的条件是:a<-1且a≠-2.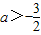
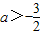 ,∴f(2)=2a+lg(a+2)+6
,∴f(2)=2a+lg(a+2)+6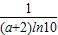 >0.
>0.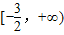 上为增函数.
上为增函数.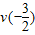 =3-lg2,∴当
=3-lg2,∴当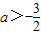 时,v(a)>
时,v(a)>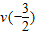 ,即f(2)>3-lg2.
,即f(2)>3-lg2.

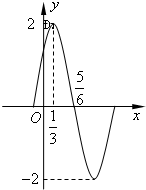 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<