
����Ŀ��2020��1��10�գ������¹ڷ��������COVID-9�����������й�����ѧ���DZ㿪ʼ�˲���������о�����.�����������ֲ��������������Ҫ��ѧ�����̣�����һ��һϦ����ɵģ�������һ����������������.��֪һ�������Ŷ���С�������������飬������������Ƿ���ֿ���.��������ǣ�ÿ�����һ�Σ�3��Ϊһ����������.��֪С������ֺ�����ֿ���ĸ���Ϊ![]() ������ÿ�ν��ֺ����Ƿ���ֿ������ϴν�����.
������ÿ�ν��ֺ����Ƿ���ֿ������ϴν�����.
��1����һ�����������ڳ��ֿ������![]() �ķֲ��У�
�ķֲ��У�
��2����֪ÿ�����һ�λ���100Ԫ�����������������鷽����
������һ����������������2�γ��ֿ��弴��ֹ���������飬������һ�������ڣ�������������������ڣ���������鷽ʽ�Ļ���Ϊ![]() Ԫ��
Ԫ��
������һ�����������ڳ���2�λ�3�ο��壬�����ڽ�������ֹ���飬��֪����������������������ڣ���������鷽ʽ�Ļ���Ϊ![]() Ԫ.
Ԫ.
�Ƚ��������![]() ��
��![]() ����ѧ�����Ĵ�С.
����ѧ�����Ĵ�С.
���𰸡���1���ֲ��д𰸼�����.��2��![]()
��������
��1���������֪���������![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]() ����
����![]() ��Ȼ���г��ֲ��м���
��Ȼ���г��ֲ��м���
��2����������ֱ����![]() ��
��![]() ����������.
����������.
��1���������֪���������![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]() ��
��
��![]() .
.
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��2������һ���������ڵĽ��ַ���Ϊ![]() Ԫ����
Ԫ����![]() ���ܵ�ȡֵΪ200��300��
���ܵ�ȡֵΪ200��300��
��Ϊ![]() ��
��![]() ��
��
����![]() .
.
���������������ڵ�ƽ������Ϊ![]() .
.
���������![]() ���ܵ�ȡֵΪ300��600��900��
���ܵ�ȡֵΪ300��600��900��
���¼�![]() Ϊ����һ�����������ڳ���2�λ�3�ο��塱���ɣ�1��֪��
Ϊ����һ�����������ڳ���2�λ�3�ο��塱���ɣ�1��֪��![]() .
.
����![]() ��
��
![]() ��
��
![]() ��
��
����![]() .
.
����![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2��֤������a��3ʱ������![]() ����ֻ��������㣮
����ֻ��������㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������![]() �����ֱ��������
�����ֱ��������![]() ���ڵ�ƽ�滥�ഹֱ.
���ڵ�ƽ�滥�ഹֱ.![]()
![]() ,
,![]() ��
��![]() .
.
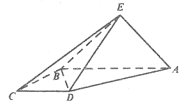
��1����֤��![]() ��
��
��2����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��3���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ
��ʹ![]() ƽ��
ƽ��![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��)(2017����ˮ��ģ)ij�̳���Ԫ�����й���齱��������涨�˿ʹ�װ�б��0,1,2,3,4�������ͬС��ij齱����һ��������������С����ȡ��������С��ı��֮�͵���7����һ�Ƚ�������6��5���ж��Ƚ�������4�������Ƚ���������Ϊ���н�.
(1)���ж��Ƚ��ĸ��ʣ�
(2)���н��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. ���⡰��![]() ����
����![]() ���ķ������ǡ���
���ķ������ǡ���![]() ����
����![]() ��
��
B. ���⡰![]() ��
��![]() ���ķ��ǡ�
���ķ��ǡ�![]() ��
��![]() ��
��
C. ��![]() ��
��![]() ���м�ֵ���ǡ�
���м�ֵ���ǡ�![]() ���ij�Ҫ����
���ij�Ҫ����
D. ���⡰������![]() ����㣬��
����㣬��![]() ��
��![]() �����������������
�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ae2x+(a��2) ex��x.
ae2x+(a��2) ex��x.
��1������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ��������㣬��a��ȡֵ��Χ.
��������㣬��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() �����ֵ��
�����ֵ��
��2����![]() ʱ������
ʱ������![]() ����Сֵ. ��
����Сֵ. ��![]() ����СֵΪ
����СֵΪ![]() ������
������![]() ��ֵ��.
��ֵ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
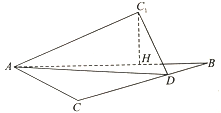
����Ŀ����ͼ���ڵ���![]() �У�б��
���![]() ��
��![]() Ϊֱ�DZ�
Ϊֱ�DZ�![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ��ֱ��
��ֱ��![]() �۵���
�۵���![]() ��λ�ã�ʹ�õ�
��λ�ã�ʹ�õ�![]() ��ƽ��
��ƽ��![]() �⣬�ҵ�
�⣬�ҵ�![]() ��ƽ��
��ƽ��![]() �ϵ���Ӱ
�ϵ���Ӱ![]() ���߶�
���߶�![]() ����
����![]() ����
����![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() �� ����
�� ����![]() ����,
����, ![]() ��
��![]() .
.
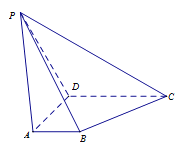
������֤��![]() ƽ��
ƽ��![]() ��
��
������֤��![]() ƽ��
ƽ��![]() ��
��
������![]() ����
����![]() ���е㣬��֤��������
���е㣬��֤��������![]() ������һ��
������һ��![]() ��
��![]() ��
��![]() ����ƽ��
����ƽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com