练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．经过点A（1，-1）与直线x-2y+1=0垂直的直线方程2x+y-1=0．

    分析 根据所求直线方程与直线x-2y+1=0垂直，设出直线方程，把点A坐标代入，即可得出所求直线方程．

    解答 解：所求直线方程与直线x-2y+1=0垂直，
    ∴设方程为2x+y+c=0，
    ∵直线过点A（1，-1），
    ∴2×1+1×（-1）+c=0，
    解得c=-1；
    ∴所求的直线方程为2x+y-1=0．
    故答案为：2x+y-1=0．

    点评 本题考查了求直线方程的应用问题，也考查了两条直线垂直的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．命题“对任意的x∈R，x3-1≤0”的否定是（　　）
    A．不存在x∈R，x3-1≤0B．存在x∈R，x3-1≤0
    C．存在x∈R．x3-1＞0D．对任意的x∈R，x3-1＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．己知程序框图如图所示，执行相应程序，若输出S=15，则框图中①处可以填入（　　）
    A．n≥4？B．n＞8？C．n＞4？D．n≥8？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若$\frac{-1-\sqrt{3}i}{2}$是方程x2+px+1=0的一个根，则p=（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

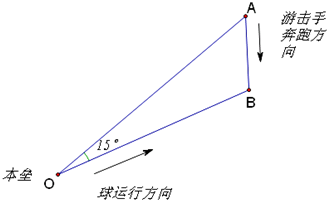    4．在奥运会垒球比赛前，C国教练布置战术时，要求击球手以与连结本垒及游击手的直线成15°的方向把球击出，根据经验及测速仪的显示，通常情况下球速为游击手最大跑速的4倍，问按这样的布置，游击手能不能接着球？（如图所示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设函数f（x）=kax-a-x（a＞0且a≠1）是定义域为R的奇函数．
    （1）若f（1）＞0，求不等式f（x2+2x）+f（x-4）＞0的解集．
    （2）已知f（1）=$\frac{3}{2}$，若存在x∈[1，+∞），使得a2x+a-2x-4mf（x）=0成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．电视台在“欢乐今宵”节目中拿出两个信箱，其中放着竞猜中成绩优秀的观众的来信，甲信箱中有30封，乙信箱中有20封，现由主持人抽奖确定幸运观众，若先确定一名幸运之星，再从两信箱中各确定一名幸运观众，有多少种不同的结果？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=-2x2+4mx-1
    （1）若m=2，θ∈（0，$\frac{π}{2}$），求$\frac{f（sinθ）}{sinθ}$的最大值
    （2）若对于任意的x∈[-1，1]，y=f（x）的最大值为7，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知sin2α=$\frac{2\sqrt{3}}{3}$sinα，α∈（0，π），则sin2α=$\frac{2\sqrt{2}}{3}$．

    查看答案和解析>>

    同步练习册答案