
【题目】已知![]() ,用符号
,用符号![]() 表示不超过
表示不超过![]() 的最大整数,若函数
的最大整数,若函数![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由f(x)=0得![]() a,令g(x)
a,令g(x)![]() ,分x>0和x<0的情况讨论,作出g(x)的图象,利用数形结合即可得到a的取值范围.
,分x>0和x<0的情况讨论,作出g(x)的图象,利用数形结合即可得到a的取值范围.
由f(x)![]() a=0得
a=0得![]() a,
a,
设g(x)![]() ,
,
则当0<x<1,[x]=0,此时g(x)=0,
当1≤x<2,[x]=1,此时g(x)![]() ,此时
,此时![]() g(x)≤1,
g(x)≤1,
当2≤x<3,[x]=2,此时g(x)![]() ,此时
,此时![]() g(x)≤1,
g(x)≤1,
当3≤x<4,[x]=3,此时g(x)![]() ,此时
,此时![]() g(x)≤1,
g(x)≤1,
当4≤x<5,[x]=4,此时g(x)![]() ,此时
,此时![]() g(x)≤1,
g(x)≤1,
若当﹣1≤x<0,[x]=﹣1,此时g(x)![]() ,此时g(x)
,此时g(x)![]() 1,
1,
若当﹣2≤x<﹣1,[x]=﹣2,此时g(x)![]() ,此时1≤g(x)
,此时1≤g(x)![]() 2,
2,
若当﹣3≤x<﹣2,[x]=﹣3,此时g(x)![]() ,此时1≤g(x)
,此时1≤g(x)![]() ,
,
若当﹣4≤x<﹣3,[x]=﹣4,此时g(x)![]() ,此时1≤g(x)
,此时1≤g(x)![]() ,
,
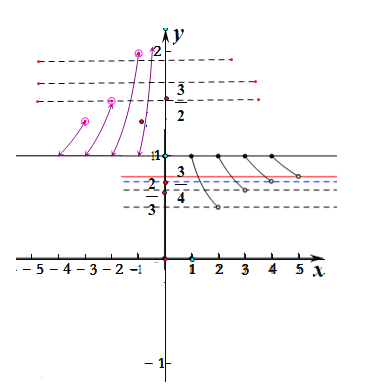
作出函数g(x)的图象,
要使f(x)![]() a有且仅有两个零点,
a有且仅有两个零点,
即函数g(x)=a有且仅有两个零点,
则由图象可知![]() 或
或![]() ,
,
故选:A.


科目:高中数学 来源: 题型:
【题目】定义在实数集![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() ,
,
则下列四个命题:①![]() ;
;
②函数![]() 的最小正周期为
的最小正周期为![]() ;
;
③当![]() 时,方程
时,方程![]() 有
有![]() 个根;
个根;
④方程![]() 有
有![]() 个根.
个根.
其中真命题的序号为________________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个班级,一次数学考试的分数排序如下:
甲班 51 54 59 60 64 68 68 68 70 71
72 72 74 76 77 78 79 79 80 80
82 85 85 86 86 87 87 87 88 89
90 90 91 96 97 98 98 98 100 100
乙班 61 63 63 66 70 71 71 73 75 75
76 79 79 80 80 80 81 81 82 82
83 83 83 84 84 84 85 85 85 85
85 85 86 87 87 88 90 91 94 98
请你就这次考试成绩,对两个班级的数学学习情况进行评价
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(Ⅰ)求证:PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE;
(Ⅲ)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司对以下两个项目进行前期市场调研:项目![]() :通信设备.根据调研,投资到该项目上,所有可能结果为:获利
:通信设备.根据调研,投资到该项目上,所有可能结果为:获利![]() 、损失
、损失![]() 、不赔不赚,且这三种情况发生的概率分别为
、不赔不赚,且这三种情况发生的概率分别为![]() ;项目
;项目![]() :新能源汽车.根据调研,投资到该项目上,所有可能结果为:获利
:新能源汽车.根据调研,投资到该项目上,所有可能结果为:获利![]() 、亏损
、亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() .经测算,当投入
.经测算,当投入![]() 两个项目的资金相等时,它们所获得的平均收益(即数学期望)也相等.
两个项目的资金相等时,它们所获得的平均收益(即数学期望)也相等.
(1)求![]() 的值;
的值;
(2)若将![]() 万元全部投到其中的一个项目,请你从投资回报稳定性考虑,为投资公司选择一个合理的项目,并说明理由.
万元全部投到其中的一个项目,请你从投资回报稳定性考虑,为投资公司选择一个合理的项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表中的数表为“森德拉姆筛”(森德拉姆,东印度学者),其特点是每行每列都成等差数列.
2 | 3 | 4 | 5 | 6 | 7 | … |
3 | 5 | 7 | 9 | 11 | 13 | … |
4 | 7 | 10 | 13 | 16 | 19 | … |
5 | 9 | 13 | 17 | 21 | 25 | … |
6 | 11 | 16 | 21 | 26 | 31 | … |
7 | 13 | 19 | 25 | 31 | 37 | … |
… | … | … | … | … | … | … |
在上表中,2017出现的次数为( )
A. 18 B. 36 C. 48![]() D. 72
D. 72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)若直线![]() 且曲线
且曲线![]() 在A处的切线与
在A处的切线与![]() 在B处的切线相互平行,求a的取值范围;
在B处的切线相互平行,求a的取值范围;
(Ⅱ)设![]() 在其定义域内有两个不同的极值点
在其定义域内有两个不同的极值点![]() 且
且![]() 若不等式
若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.在极坐标系中有射线
轴的正半轴为极轴建立极坐标系.在极坐标系中有射线![]() 和曲线
和曲线![]() .
.
(1)判断射线![]() 和曲线
和曲线![]() 公共点的个数;
公共点的个数;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com