
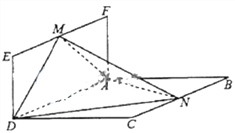
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,四边形
为菱形,四边形![]() 为矩形,
为矩形, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的长.
的长.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直线![]() 与
与![]() 相交于
相交于![]() 两点,且满足:①
两点,且满足:①![]() 与
与![]() (
(![]() 为坐标原点)的斜率之和为2;②直线
为坐标原点)的斜率之和为2;②直线![]() 与圆
与圆![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n是两条不同的直线,α,β是两个不重合的平面,给定下列四个命题,其中为真命题的是( ) ① ![]() ;②
;② ![]() ;
;
③ ![]() ;④
;④  .
.
A.①和②
B.②和③
C.③和④
D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=2py(p>0)与直线2x﹣y+1=0交于A,B两点, ![]() ,点M在抛物线上,MA⊥MB.
,点M在抛物线上,MA⊥MB. 
(1)求p的值;
(2)求点M的横坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=(log2x)2﹣2alog2x+b(x>0).当x= ![]() 时,f(x)有最小值﹣1.
时,f(x)有最小值﹣1.
(1)求a与b的值;
(2)求满足f(x)<0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c,且f(﹣3)=f(1),f(0)=0.
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)﹣(4+2a)x+2,x∈[1,2],求函数g(x)的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com