
【题目】已知![]() 的图象关于原点对称,其中a为常数.
的图象关于原点对称,其中a为常数.
(1)求a的值,并写出函数f(x)的单调区间(不需要求解过程);
(2)若关于x的方程![]() 在[2,3]上有解,求k的取值范围.
在[2,3]上有解,求k的取值范围.
【答案】(1)![]() ,f(x)在(﹣∞,﹣1)和(1,+∞)上是单调增函数;(2)[﹣1,1].
,f(x)在(﹣∞,﹣1)和(1,+∞)上是单调增函数;(2)[﹣1,1].
【解析】
(1)根据![]() 的图象关于原点对称,得到f(x)是奇函数,
的图象关于原点对称,得到f(x)是奇函数,
则f(x)+f(﹣x)=0,恒成立,即![]() 恒成立,化简为x2(a2﹣1)=0求解.根据a的值,f(x)=log
恒成立,化简为x2(a2﹣1)=0求解.根据a的值,f(x)=log![]() (1
(1![]() ),再利用复合函数的单调性确定单调区间.
),再利用复合函数的单调性确定单调区间.
(2)关于x的方程![]() 在[2,3]上有解,即
在[2,3]上有解,即![]() (x+k)在[2,3]上有解,转化为k
(x+k)在[2,3]上有解,转化为k![]() x,在[2,3]上有解,再求得g(x)
x,在[2,3]上有解,再求得g(x)![]() x,x∈[2,3]值域即可.
x,x∈[2,3]值域即可.
(1)因为![]() 的图象关于原点对称,
的图象关于原点对称,
所以f(x)为奇函数,
所以f(x)+f(﹣x)=0,
即![]() ,
,
所以1﹣a2x2=1-x2,
即x2(a2﹣1)=0,
所以a=﹣1或a=1(舍去),
所以f(x)=log![]() (1
(1![]() ),定义域为(﹣∞,﹣1)
),定义域为(﹣∞,﹣1)![]() (1,+∞).
(1,+∞).
所以f(x)的增区间是(﹣∞,﹣1)和(1,+∞),无减区间.
(2)关于x的方程![]() 在[2,3]上有解,
在[2,3]上有解,
即![]() (x+k)在[2,3]上有解,
(x+k)在[2,3]上有解,
即![]() x+k,得k
x+k,得k![]() x,
x,
令g(x)![]() x,x∈[2,3],
x,x∈[2,3],
则g(x)=1![]() x在x∈[2,3]上单调递减,且f(2)=1,f(3)=﹣1,
x在x∈[2,3]上单调递减,且f(2)=1,f(3)=﹣1,
所以k的取值范围是[﹣1,1].


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
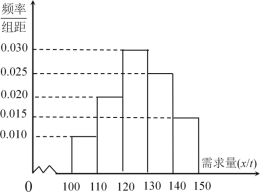
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了培养学生的安全意识,某中学举行了一次“安全自救”的知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题:
序号(i) | 分组(分数) | 组中值(Gi) | 频数(人数) | 频率(fi) |
1 |
| 65 | ① | 0.10 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.20 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1.00 | ||
(1)求出频率分布表中①②③④⑤处的值;
(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生能获奖;
(3)求这800名学生的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点坐标分别是
的两个焦点坐标分别是![]() 、
、![]() ,并且经过点
,并且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() :
:![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() .当
.当![]() ,且满足
,且满足![]() 时,求
时,求![]() 面积
面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,称
,称![]() 为函数
为函数![]() 的不动点.有下面三个命题:(1)若
的不动点.有下面三个命题:(1)若![]() 是二次函数,且没有不动点,则函数
是二次函数,且没有不动点,则函数![]() 也没有不动点;(2)若
也没有不动点;(2)若![]() 是二次函数,则函数
是二次函数,则函数![]() 可能有
可能有![]() 个不动点;(3)若
个不动点;(3)若![]() 的不动点的个数是
的不动点的个数是![]() ,则
,则![]() 的不动点的个数不可能是
的不动点的个数不可能是![]() ;它们中所有真命题的序号是________________________.
;它们中所有真命题的序号是________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欧拉公式![]() (
(![]() 为虚数单位,
为虚数单位,![]() ,
,![]() 为自然底数)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,
为自然底数)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,![]() 表示的复数在复平面中位于( )
表示的复数在复平面中位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com