
【题目】下列说法正确的是:
①在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差;
②回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
③在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量
中,当解释变量每增加1个单位时,预报变量![]() 平均增加0.1个单位
平均增加0.1个单位
④若![]() ,
,![]() ,则
,则![]() ;
;
⑤已知正方体![]() ,
,![]() 为底面
为底面![]() 内一动点,
内一动点,![]() 到平面
到平面![]() 的距离与到直线
的距离与到直线![]() 的距离相等,则
的距离相等,则![]() 点的轨迹是抛物线的一部分.
点的轨迹是抛物线的一部分.
正确的序号是:______.
【答案】②③④⑤
【解析】
根据回归分析概念及回归系数的含义,可判定①不正确;②是正确的;③是正确的;由三角恒等变换的公式,可判定④是正确的;根据正方体结构特征和抛物线的定义以⑤是正确的.
对于①中,在做回归分析时,由残差图中残差点分布的带状区域的宽度越窄表示回归效果越好,所以①不正确;
对于②中,回归分析模型中,残差平方和越小,说明模型的拟合效果越好是正确的,所以②是正确的;
对于③中,在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量
中,当解释变量每增加1个单位时,预报变量![]() 平均增加0.1个单位,所以③是正确的.
平均增加0.1个单位,所以③是正确的.
对于④中,若![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
解得![]() ,所以
,所以![]() ,所以④是正确的;
,所以④是正确的;
⑤在正方体![]() ,则
,则![]() 是点
是点![]() 到直线
到直线![]() 的距离,过
的距离,过![]() 作
作![]() 垂直于直线
垂直于直线![]() ,则
,则![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
因为![]() 到平面
到平面![]() 的距离到直线
的距离到直线![]() 的距离,所以
的距离,所以![]() ,
,
根据抛物线的定义,可得点![]() 的轨迹是抛物线的一部分,所以⑤是正确的.
的轨迹是抛物线的一部分,所以⑤是正确的.

故答案为:②③④⑤.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )经过点
)经过点![]() ,且两个焦点
,且两个焦点![]() ,
,![]() 的坐标依次为
的坐标依次为![]() 和
和![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,证明:直线
,证明:直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为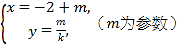 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com