练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】南北朝时代的伟大科学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”. 其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面α所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等.如图，夹在两个平行平面之间的两个几何体的体积分别为V1,V2，被平行于这两个平面的任意平面截得的两个截面面积分别为S1,S2，则（ ）

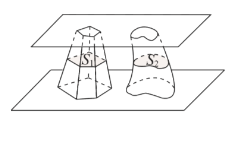
    A.如果S1,S2总相等，则V1=V2

    B.如果S1=S2总相等，则V1与V2不一定相等

    C.如果V1=V2 ，则S1,S2总相等

    D.存在这样一个平面α使S1=S2相等，则V1=V2

    【答案】A

    【解析】

    由祖暅原理的含义直接判断即可得出答案.

    如图所示：

    由祖暅原理的含义可得当平面，并且和平行的平面截得两个几何体的所得的截面面积时，，则A选项正确.

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】过抛物线的焦点的直线交抛物线于两点，分别过作准线的垂线，垂足分别为两点，以为直径的圆过点，则圆的方程为( )

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某校高三的学生中随机抽取了100名学生，统计了某次数学模考考试成绩如表：

    （1）请在频率分布表中的①、②位置上填上相应的数据，并在给定的坐标系中作出这些数据的频率分布直方图，再根据频率分布直方图估计这100名学生的平均成绩；

    （2）从这100名学生中，采用分层抽样的方法已抽取了 20名同学参加“希望杯数学竞赛”，现需要选取其中3名同学代表高三年级到外校交流，记这3名学生中“期中考试成绩低于120分”的人数为，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

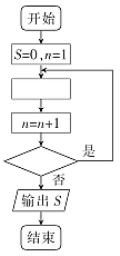
    【题目】在印度有一个古老的传说：舍罕王打算奖赏国际象棋的发明人一宰相西萨·班·达依尔．国王问他想要什么，他对国王说：“陛下，请您在这张棋盘的第1个小格里，赏给我1粒麦子，在第2个小格里给2粒，第3小格给4粒，以后每1小格都比前1小格加1倍．请您把这样摆满棋盘上所有的64格的麦粒，都赏给您的仆人吧！”国王觉得这要求太容易满足了，就同意给他这些麦粒．当人们把一袋一袋的麦子搬来开始计数时，国王才发现就是把全印度甚至全世界的麦粒全拿来，也满足不了那位宰相的要求．那么，宰相要求得到的麦粒到底有多少粒？如图所示的程序框图是为了计算上面这个问题而设计的，那么在“”和“”中，可以先后填入（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“郑一”号宇宙飞船返回舱顺利到达地球后，为了及时将航天员救出，地面指挥中心的在返回舱预计到达的区域安排了同一条直线上的三个救援中心（记为）．当返回舱距地面1万米的点的时（假定以后垂直下落，并在点着陆），救援中心测得飞船位于其南偏东60°方向，仰角为60°，救援中心测得飞船位于其南偏西30°方向，仰角为30°，救援中心测得着陆点位于其正东方向．

    （1）求两救援中心间的距离；

    （2）救援中心与着陆点间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

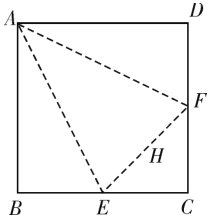
    【题目】如图，在边长为2的正方形中，，分别为，的中点，为的中点，沿，，将正方形折起，使，，重合于点，在构成的四面体中，下列结论中错误的是（ ）

    A. 平面

    B. 直线与平面所成角的正切值为

    C. 异面直线和求所成角为

    D. 四面体的外接球表面积为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2016·威海模拟)三人参加某娱乐闯关节目，假设甲闯关成功的概率是，乙、丙两人同时闯关成功的概率是，甲、丙两人同时闯关失败的概率是，且三人各自能否闯关成功相互独立．

    (1)求乙、丙两人各自闯关成功的概率；

    (2)设ξ表示三人中最终闯关成功的人数，求ξ的分布列和均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】广场舞是现代城市群众文化、娱乐发展的产物，也是城市精神文明建设成果的一个重要象征.2018年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查，随机抽取了40名广场舞者进行调查，将他们年龄分成6段：，，，，，后得到如图所示的频率分布直方图.

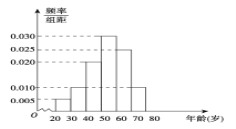
    （1）根据广场舞者年龄的频率分布直方图，估计广场舞者的平均年龄；

    （2）若从年龄在内的广场舞者中任取2名，求选中的两人中恰有一人年龄在内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大型高端制造公司为响应《中国制造2025》中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据：

    （1)根据数据可知与之间存在线性相关关系

    (i)求出关于的线性回归方程(系数精确到);

    (ii)若2018年6月份研发投人为25百万元,根据所求的线性回归方程估计当月产品的销量；

    （2）为庆祝该公司9月份成立30周年,特制定以下奖励制度:以(单位:万台)表示日销量, ,则每位员工每日奖励元；,则每位员工每日奖励元；,则每位员工每日奖励元现已知该公司9月份日销量 (万台)服从正态分布,请你计算每位员工当月(按天计算)获得奖励金额总数大约多少元.

    参考数据: ，.

    参考公式:对于一组数据,,其回归直线的斜率和截距的最小二乘估计分别为: ，.

    若随机变量服从正态分布,则 .

    查看答案和解析>>

    同步练习册答案