
【题目】若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
①y= ![]() ;②y=
;②y=  ;③y=
;③y= ![]() ;④y=
;④y=  .
.
【答案】②③
【解析】解:①函数y=﹣x﹣1,(x<0)关于原点对称的函数为﹣y=x﹣1,即y=﹣x+1,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数只有一个,所以函数f(x)的“伙伴点组”有1个,不满足条件.
②函数y=﹣ln|x|(x<0)关于原点对称的函数为﹣y=﹣ln|﹣x|,即y=ln|x|,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.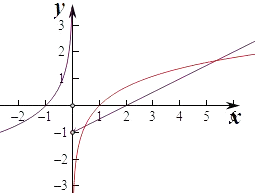
③函数y=﹣x2﹣4x,(x<0)关于原点对称的函数为﹣y=﹣x2+4x,即y=x2﹣4x,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有2个,所以函数f(x)的“伙伴点组”有2个,满足条件.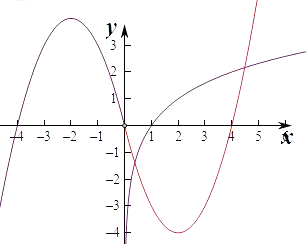
④函数y=e﹣x , (x<0)关于原点对称的函数为﹣y=ex , 即y=﹣ex ,
在x>0上作出两个函数的图象如图,
由图象可知两个函数在x>0上的交点个数有0个,所以函数f(x)的“伙伴点组”有0个,不满足条件.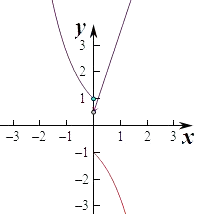 ,
,
所以答案是:②③.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的焦距为
的焦距为 ![]() ,且过点
,且过点 ![]() ,设
,设 ![]() ,
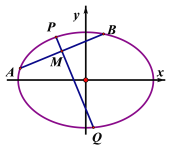
,![]() 是
是 ![]() 上的两个动点,线段
上的两个动点,线段 ![]() 的中点
的中点 ![]() 的横坐标为
的横坐标为 ![]() ,线段
,线段 ![]() 的中垂线交椭圆
的中垂线交椭圆 ![]() 于
于 ![]() ,
,![]() 两点.
两点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设![]() 点纵坐标为m,求直线
点纵坐标为m,求直线![]() 的方程,并求出
的方程,并求出 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内两点P,Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是(填空写所有正确选项的序号)
①y= ![]() ;②y=
;②y=  ;③y=
;③y= ![]() ;④y=
;④y=  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() .
.
(1)用含a的式子表示b;
(2)令F(x)= ![]() ,其图象上任意一点P(x0 , y0)处切线的斜率
,其图象上任意一点P(x0 , y0)处切线的斜率 ![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若a=2,试求f(x)在区间 ![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).

(1)求对角线![]() 所在直线的方程;
所在直线的方程;
(2)求矩形![]() 外接圆的方程;
外接圆的方程;
(3)若动点![]() 为外接圆上一点,点
为外接圆上一点,点![]() 为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人各有相同的小球10个,在每人的10个小球中都有5个标有数字1,3个标有数字2,2个标有数字3。两人同时分别从自己的小球中任意抽取1个,规定:若抽取的两个小球上的数字相同,则甲获胜,否则乙获胜,求乙获胜的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fn(x)=﹣xn+3ax(a∈R,n∈N+),若对任意的x1 , x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,则a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是_____________.
①.如果命题“![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题.
一定是真命题.
②.命题![]() ,则
,则![]()
③.命题“若![]() ,则
,则![]() ”的否命题是:“若
”的否命题是:“若![]() ,则
,则![]() ”
”
④.特称命题 “![]() ,使
,使![]() ”是真命题.
”是真命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com