
分析 (1)令x1>x2且x1,x2∈R,有f(x1)•f(x2-x1)=f(x2),又x2-x1<0,即f(x2-x1)>1故$\frac{{f({x_2})}}{{f({x_1})}}=f({x_2}-{x_1})>1$,从而确定f(x1)与f(x2)的大小,根据函数单调性的定义进行判定即可;
(2)由f(4)=$\frac{1}{16}=f(2+2)={f^2}$(2)⇒故f(2)=$\frac{1}{4}$,不等式可变形为f(x2-3x+2)≤f(2)即x2-3x≥0,从而求解.
解答 (1)证明:令x1>x2且x1,x2∈R
有f(x1)•f(x2-x1)=f(x2),又x2-x1<0,即f(x2-x1)>1
故$\frac{{f({x_2})}}{{f({x_1})}}=f({x_2}-{x_1})>1$,又f(x)>0∴f(x2)>f(x1)
故f(x)为R上的减函数; …(6分)
(2)f(4)=$\frac{1}{16}=f(2+2)={f^2}$(2)⇒故f(2)=$\frac{1}{4}$,…(8分)
则原不等式可变形为f(x2-3x+2)≤f(2)
即x2-3x≥0------------(10分)
解得:x≥3或x≤0------------(12分)
点评 以及灵活利用所给的恒等式证明函数的单调性,及利用单调性解不等式问题.此类题要求答题者有较高的数学思辨能力,能从所给的条件中寻找到证明问题的关键点出来.属于中档题.


科目:高中数学 来源: 题型:解答题
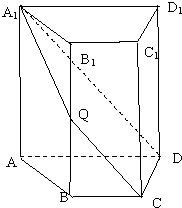 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为梯形,AD∥BC,AD=2BC,过 A1,C,D三点的平面记为α,BB1与α的交点为Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{16}{65}$ | B. | $\frac{56}{65}$ | C. | $\frac{16}{65}$ | D. | -$\frac{56}{65}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com