
分析 (1)根据假设他通过考核选拔进入该校的“摄影”、“棋类”、“国学”三个社团的概率依次为m,$\frac{1}{3}$,n,已知三个社团他都能进入的概率为$\frac{1}{24}$,至少进入一个社团的概率为$\frac{3}{4}$,且m>n,建立方程组,即可求m与n的值;
(2)确定学分X的可能取值,求出相应的概率,可得X的分布列与数学期望
解答 解:(1)由题意,$\left\{\begin{array}{l}{\frac{1}{3}mn=\frac{1}{24}}\\{1-\frac{2}{3}(1-m)(1-n)=\frac{3}{4}}\end{array}\right.$,m>n
∴m=$\frac{1}{2}$,n=$\frac{1}{4}$;
(2)学分X的取值分别为0,1,2,3,4,5,6,则
P(X=0)=$\frac{1}{4}$,P(X=1)=$\frac{1}{2}$×$\frac{2}{3}×\frac{3}{4}$=$\frac{1}{4}$,P(X=2)=$\frac{1}{3}$×$\frac{1}{2}×\frac{3}{4}$=$\frac{1}{8}$,P(X=3)=$\frac{1}{2}×\frac{2}{3}×$$\frac{1}{4}$+$\frac{1}{2}×\frac{1}{3}$×$\frac{3}{4}$=$\frac{5}{24}$,
P(X=4)=$\frac{1}{2}×\frac{1}{4}$×$\frac{2}{3}$=$\frac{1}{12}$,P(X=5)=$\frac{1}{2}×$$\frac{1}{3}×\frac{1}{4}$=$\frac{1}{24}$,P(X=6)=$\frac{1}{24}$.
X的分布列
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{5}{24}$ | $\frac{1}{12}$ | $\frac{1}{24}$ | $\frac{1}{24}$ |
点评 本题考查概率的求解,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
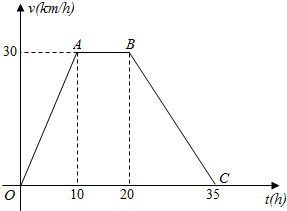 据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com