
分析 根据直线与圆相交,圆x2+y2=12可知:圆心为(0,0),半径r=2$\sqrt{3}$,弦长为|AB|=4$\sqrt{3}$=2r,说明直线l过圆心O所以可以得到直线AB的倾斜角.根据AOC和OBD是两个全等的直角三角形,OA=OB=2$\sqrt{3}$,
即可求出OC和OD,由直线的倾斜角即可得到|CD|的长度.
解答 解:由圆的方程x2+y2=12可知:圆心为(0,0),半径r=2$\sqrt{3}$,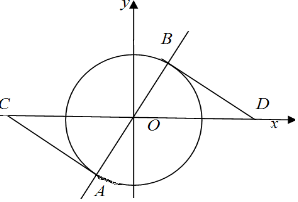
∵弦长为|AB|=4$\sqrt{3}$=2r,
∴可以得知直线l经过圆心O.
∴0=k(0-1)-$\sqrt{3}$,解得k=$\sqrt{3}$,
∴直线AB的方程为:y=$\sqrt{3}$x,
设直线AB的倾斜角为θ,则tanθ=$\sqrt{3}$,
∴θ=60°,
∴在Rt△AOC中:|CO|=$\frac{|OA|}{cos60°}$=$\frac{2\sqrt{3}}{\frac{1}{2}}$=4$\sqrt{3}$,
那么:|CD|=2|OC|=8$\sqrt{3}$,
故答案为:8$\sqrt{3}$.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ?x,y∈R,x2+y2<0 | B. | ?x,y∈R,x2+y2≤0 | ||
| C. | ?x0,y0∈R,x02+y02≤0 | D. | ?x0,y0∈R,x02+y02<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
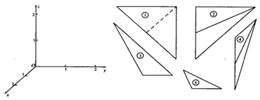 在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标系分别为(0,0,2),(2,2,2),(2,2,0),(2,1,1),给出编号为①②③④⑤的五个图,则该四面体的侧视图和俯视图分别为( )
在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标系分别为(0,0,2),(2,2,2),(2,2,0),(2,1,1),给出编号为①②③④⑤的五个图,则该四面体的侧视图和俯视图分别为( )| A. | ①和⑤ | B. | ②和③ | C. | ④和⑤ | D. | ④和③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 216 | B. | 168 | C. | 144 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com