
【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席.其中超算全球第一“神威·太湖之光”完全使用了国产品牌处理器.为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下:(数值越小,速度越快,单位是MIPS)

(Ⅰ)从品牌![]() 的12次测试中,随机抽取一次,求测试结果小于7的概率;
的12次测试中,随机抽取一次,求测试结果小于7的概率;
(Ⅱ)从12次测试中,随机抽取三次,记![]() 为品牌
为品牌![]() 的测试结果大于品牌
的测试结果大于品牌![]() 的测试结果的次数,求
的测试结果的次数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
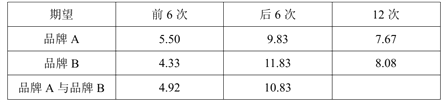
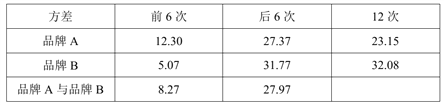
(Ⅲ)经过了解,前6次测试是打开含有文字与表格的文件,后6次测试时打开含有文字与图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
【答案】(Ⅰ)![]() (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析
【解析】试题分析:(1)利用古典概型公式计算测试结果小于7的概率;(2) 明确12次测试中,品牌![]() 的测试结果大于品牌
的测试结果大于品牌![]() 的测试结果的次数,得到相应的概率值,列表,求出期望;(3)运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
的测试结果的次数,得到相应的概率值,列表,求出期望;(3)运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
试题解析:
(Ⅰ)从品牌![]() 的12次测试中,测试结果打开速度小于7的文件有:
的12次测试中,测试结果打开速度小于7的文件有:
测试1、2、5、6、9、10、11,共7次
设该测试结果打开速度小于7为事件![]() ,因此
,因此![]()
(Ⅱ)12次测试中,品牌![]() 的测试结果大于品牌
的测试结果大于品牌![]() 的测试结果的次数有:
的测试结果的次数有:
测试1、3、4、5、7、8,共6次
随机变量![]() 所有可能的取值为:0,1,2,3
所有可能的取值为:0,1,2,3
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
随机变量![]() 的分布列为
的分布列为

![]() ,
,
(Ⅲ)本题为开放问题,答案不唯一,在此给出评价标准,并给出可能出现的答案情况,给出明确结论,
结合已有数据,能够运用以下8个标准中的任何一个陈述得出该结论的理由,
标准1:会用前6次测试品牌![]() 、品牌
、品牌![]() 的测试结果的平均值与后6次测试品牌
的测试结果的平均值与后6次测试品牌![]() 、品牌
、品牌![]() 的测试结果的平均值进行阐述(这两种品牌的处理器打开含有文字与表格的文件的测试结果的平均值均小于打开含有文字和图片的文件的测试结果平均值;这两种品牌的处理器打开含有文字与表格的文件的平均速度均快于打开含有文字和图片的文件的平均速度)
的测试结果的平均值进行阐述(这两种品牌的处理器打开含有文字与表格的文件的测试结果的平均值均小于打开含有文字和图片的文件的测试结果平均值;这两种品牌的处理器打开含有文字与表格的文件的平均速度均快于打开含有文字和图片的文件的平均速度)
标准2:会用前6次测试品牌![]() 、品牌
、品牌![]() 的测试结果的方差与后6次测试品牌
的测试结果的方差与后6次测试品牌![]() 、品牌
、品牌![]() 的测试结果的方差进行阐述(这两种品牌的处理器打开含有文字与表格的文件的测试结果的方差均小于打开含有文字和图片的文件的测试结果的方差;这两种品牌的处理器打开含有文字与表格的文件速度的波动均小于打开含有文字和图片的文件速度的波动)
的测试结果的方差进行阐述(这两种品牌的处理器打开含有文字与表格的文件的测试结果的方差均小于打开含有文字和图片的文件的测试结果的方差;这两种品牌的处理器打开含有文字与表格的文件速度的波动均小于打开含有文字和图片的文件速度的波动)
标准3:会用品牌![]() 前6次测试结果的平均值、后6次测试结果的平均值与品牌
前6次测试结果的平均值、后6次测试结果的平均值与品牌![]() 前6次测试结果的平均值、后6次测试结果的平均值进行阐述(品牌
前6次测试结果的平均值、后6次测试结果的平均值进行阐述(品牌![]() 前6次测试结果的平均值大于品牌
前6次测试结果的平均值大于品牌![]() 前6次测试结果的平均值,品牌
前6次测试结果的平均值,品牌![]() 后6次测试结果的平均值小于品牌
后6次测试结果的平均值小于品牌![]() 后6次测试结果的平均值,品牌
后6次测试结果的平均值,品牌![]() 打开含有文字和表格的文件的速度慢于品牌
打开含有文字和表格的文件的速度慢于品牌![]() ,品牌
,品牌![]() 打开含有文字和图形的文件的速度快于品牌
打开含有文字和图形的文件的速度快于品牌![]() )
)
标准4:会用品牌![]() 前6次测试结果的方差、后6次测试结果的方差与品牌
前6次测试结果的方差、后6次测试结果的方差与品牌![]() 前6次测试结果的方差、后6次测试结果的方差进行阐述(品牌
前6次测试结果的方差、后6次测试结果的方差进行阐述(品牌![]() 前6次测试结果的方差大于品牌
前6次测试结果的方差大于品牌![]() 前6次测试结果的方差,品牌
前6次测试结果的方差,品牌![]() 后6次测试结果的方差小于品牌
后6次测试结果的方差小于品牌![]() 后6次测试结果的方差,品牌
后6次测试结果的方差,品牌![]() 打开含有文字和表格的文件的速度波动大于品牌
打开含有文字和表格的文件的速度波动大于品牌![]() ,品牌
,品牌![]() 打开含有文字和图形的文件的速度波动小于品牌
打开含有文字和图形的文件的速度波动小于品牌![]() )
)
标准5:会用品牌![]() 这12次测试结果的平均值与品牌
这12次测试结果的平均值与品牌![]() 这12次测试结果的平均值进行阐述(品牌
这12次测试结果的平均值进行阐述(品牌![]() 这12次测试结果的平均值小于品牌
这12次测试结果的平均值小于品牌![]() 这12次测试结果的平均值,品牌
这12次测试结果的平均值,品牌![]() 打开文件的平均速度快于
打开文件的平均速度快于![]() )
)
标准6:会用品牌![]() 这12次测试结果的方差与品牌
这12次测试结果的方差与品牌![]() 这12次测试结果的方差进行阐述(品牌
这12次测试结果的方差进行阐述(品牌![]() 这12次测试结果的方差小于品牌
这12次测试结果的方差小于品牌![]() 这12次测试结果的方差,品牌
这12次测试结果的方差,品牌![]() 打开文件速度的波动小于
打开文件速度的波动小于![]() )
)
标准7:会用前6次测试中,品牌![]() 测试结果大于(小于)品牌
测试结果大于(小于)品牌![]() 测试结果的次数、后6次测试中,品牌
测试结果的次数、后6次测试中,品牌![]() 测试结果大于(小于)品牌
测试结果大于(小于)品牌![]() 测试结果的次数进行阐述(前6次测试结果中,品牌
测试结果的次数进行阐述(前6次测试结果中,品牌![]() 小于品牌
小于品牌![]() 的有2次,占
的有2次,占![]() .后6次测试中,品牌
.后6次测试中,品牌![]() 小于品牌
小于品牌![]() 的有4次,占
的有4次,占![]() .故品牌
.故品牌![]() 打开含有文字和表格的文件的速度慢于
打开含有文字和表格的文件的速度慢于![]() ,品牌
,品牌![]() 打开含有文字和图片的文件的速度快
打开含有文字和图片的文件的速度快![]() )
)
标准8:会用这12次测试中,品牌![]() 测试结果大于(小于)品牌
测试结果大于(小于)品牌![]() 测试结果的次数进行阐述(这12次测试结果中,品牌
测试结果的次数进行阐述(这12次测试结果中,品牌![]() 小于品牌
小于品牌![]() 的有6次,占
的有6次,占![]() .故品牌
.故品牌![]() 和品牌
和品牌![]() 打开文件的速度相当)
打开文件的速度相当)
参考数据


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量, ![]() 获得本场比赛胜利,最终人机大战总比分定格
获得本场比赛胜利,最终人机大战总比分定格![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(Ⅰ)根据已知条件完成下面的列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?

非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名淡定生中的“围棋迷”人数为![]() 。若每次抽取的结果是相互独立的,求
。若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:  ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届北京市海淀区】如图,三棱柱![]() 侧面
侧面![]() 底面
底面![]() ,
, ![]()
![]()
![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
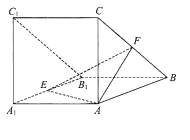
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求三棱柱![]() 的体积;
的体积;
(Ⅲ)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度得到曲线
个单位长度得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)已知![]() 为曲线
为曲线![]() 上的动点,
上的动点, ![]() 两点的极坐标分别为
两点的极坐标分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com