Question

【题目】已知椭圆的离心率为，其中左焦点(-2,0).

（1） 求椭圆C的方程；

（2） 若直线y=x+m与椭圆C交于不同的两点A，B，且线段AB的中点M在圆x2+y2=1上，求m的值.

Answer 1

【答案】19. 解①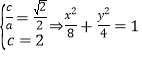

②设

由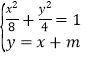

又在上

或

经检验解题

或

【解析】

本试题主要是考查了椭圆方程的求解，以及直线与椭圆的位置关系的运用。

（1）由题意，得得到a,b,c的值。得到椭圆的方程。

（2）设点A、B的坐标分别为（x1,y1),(x2, y2)，线段AB的中点为M(x0,y0)，

由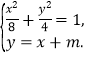消y得，3x2+4mx+2m2-8=0结合韦达定理，和判别式得到参数m值。

解：（1） 由题意，得………………………………………………3分

解得∴椭圆C的方程为.…………………………………………6分

（2） 设点A、B的坐标分别为（x1,y1),(x2, y2)，线段AB的中点为M(x0,y0)，

由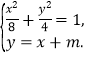消y得，3x2+4mx+2m2-8=0,……………………………………………8分

Δ=96-8m2＞0,∴-2＜m＜2.

∴.………………………………………12分

∵点M(x0,y0)在圆x2+y2=1上，

，.………………………………………………… 14分