
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,平面
是菱形,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.
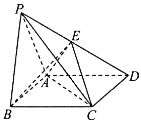
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中记载了这样的一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”,其大意为:有一个人走了378里路,第一天健步行走,从第二天起其因脚痛每天走的路程为前一天的一半,走了6天后到达了目的地,问此人第三天走的路程里数为( )
A.192B.48C.24D.88
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 在左、右顶点分别为
在左、右顶点分别为![]() 、
、![]() ,左焦点为
,左焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 和
和![]() 均不在坐标轴上),直线
均不在坐标轴上),直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() 的中点.
的中点.
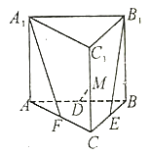
(1)证明:直线![]() 与
与![]() 共面;并求其所成角的余弦值;
共面;并求其所成角的余弦值;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,以
的上、下顶点,以![]() 为直径作圆
为直径作圆![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() (
(![]() 为坐标原点)的面积;
为坐标原点)的面积;
(2)若点![]() 、
、![]() 分别在直线
分别在直线![]() 、
、![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)证明:对任意实数![]() ,函数
,函数![]() 的图象与直线
的图象与直线![]() 最多只有一个交点;
最多只有一个交点;
(3)设![]() 若函数
若函数![]() 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的一个动点,且
上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() :
:![]() 于另一点
于另一点![]() .若
.若![]() 的面积为3,求直线
的面积为3,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com