
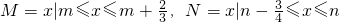 且M、N都是集合{x|0≤x≤1}的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值为
且M、N都是集合{x|0≤x≤1}的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值为



 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源:江西省宜春市高安中学2012届高三第一次段考数学理科试题 题型:022
已知a,b均为实数
,设数集A={x|a≤x≤a+查看答案和解析>>
科目:高中数学 来源:2013年浙江省温州市高一摇篮杯数学竞赛模拟试卷(二)(解析版) 题型:选择题
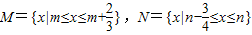 且M、N都是集合{x|0≤x≤1}的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值为( )
且M、N都是集合{x|0≤x≤1}的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值为( )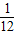

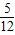

查看答案和解析>>
科目:高中数学 来源:0113 期中题 题型:单选题
 ,
, ,P={x|0≤x≤1},且M,N都是集合P的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值是
,P={x|0≤x≤1},且M,N都是集合P的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值是



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com