
| A. | tanx-tany>0 | B. | xsinx-ysiny>0 | C. | lnx+lny>0 | D. | 2x-2y>0 |
分析 利用函数单调性和特殊值依次判断选项即可.
解答 解:x,y∈R,且x>y>0,
对于A:当x=$\frac{2π}{3}$,y=$\frac{π}{3}$时,tan$\frac{2π}{3}$=$-\sqrt{3}$,tan$\frac{π}{3}$=$\sqrt{3}$,显然不成立;
对于B:当x=π,y=$\frac{π}{2}$时,πsinπ=-π,-$\frac{π}{2}$sin$\frac{π}{2}$=-1,显然不成立;
对于C:lnx+lny>0,即ln(xy)>ln1,可得xy>0,∵x>y>0,那么xy不一定大于0,显然不成立;
对于D:2x-2y>0,即2x>2y,根据指数函数的性质可知:x>y,恒成立.
故选D
点评 本题考查了各基本函数的性质以及单调性的运用.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
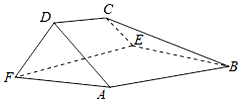 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-5或a=-15 | B. | a=-5或a=15 | C. | a=5或a=-15 | D. | a=5或a=15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
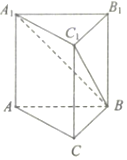 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )| A. | $\frac{8}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com