
【题目】从数列![]() 中抽出一项,依原来的顺序组成的新叫数列
中抽出一项,依原来的顺序组成的新叫数列![]() 的一个子列.
的一个子列.
(1)写出数列![]() 的一个是等比数列的子列;
的一个是等比数列的子列;
(2)若![]() 是无穷等比数列,首项
是无穷等比数列,首项![]() ,公比
,公比![]() 且
且![]() ,则数列
,则数列![]() 是否存在一个子列,为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
是否存在一个子列,为无穷等差数列?若存在,写出该子列的通项公式;若不存在,证明你的结论.
 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
【题目】从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入![]() 万元,以后每年投入将比上年减少
万元,以后每年投入将比上年减少![]() .本年度当地旅游业收入估计为
.本年度当地旅游业收入估计为![]() 万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加![]() .
.
(Ⅰ)设![]() 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为![]() 万元,旅游业总收入为
万元,旅游业总收入为![]() 万元.写出
万元.写出![]() 的表达式;
的表达式;
(Ⅱ)至少经过几年旅游业的总收入才能超过总投入?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别是a,b,c已知b=4,c=5,A=60°.
(1)求边长a和△ABC的面积;
(2)求sin2B的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目, ![]() 两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将![]() 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家![]() 队的平均分比
队的平均分比![]() 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
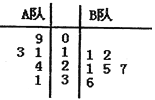
(1)根据茎叶图中的数据,求出![]() 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从![]() 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从![]() 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() ,设圆
,设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com