
【题目】已知椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,
两点,![]() 不与
不与![]() 轴垂直,圆
轴垂直,圆![]() .
.
(1)若点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值;
的最大值;
(2)若过线段![]() 的中点
的中点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
(1)由圆的几何性质得到![]() ,由两点间距离公式得到
,由两点间距离公式得到![]() ,再根据点在椭圆上二元化一元,结合二次函数的性质得到结果;(2)联立直线
,再根据点在椭圆上二元化一元,结合二次函数的性质得到结果;(2)联立直线![]() 和椭圆方程,根据韦达定理得到点
和椭圆方程,根据韦达定理得到点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,再由两直线的垂直关系得到
,再由两直线的垂直关系得到![]() 代入判别式得到参数
代入判别式得到参数![]() 的范围.
的范围.
(1)依题意,圆![]() ,即圆
,即圆![]() ,圆心为
,圆心为![]() .
.
所以![]() .
.
设![]() ,则
,则![]() .(*)
.(*)
而![]() ,所以
,所以![]() .
.
代入(*)中,可得![]() ,
,![]() .
.
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
(2)依题意,设直线![]() .
.
由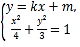 消去
消去![]() 整理得
整理得![]() .
.
因为直线与椭圆交于不同的两点,
所以![]() ,整理得
,整理得![]() .①
.①
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.
所以直线![]() 的斜率为
的斜率为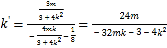 .
.
又直线![]() 和直线
和直线![]() 垂直,则
垂直,则![]() ,所以
,所以![]() .
.
将![]() 代入①式,可得
代入①式,可得![]() .
.
解得![]() 或
或![]() .
.
所以直线![]() 的斜率的取值范围为
的斜率的取值范围为![]() .
.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】以椭圆![]() 的中心O为圆心,以
的中心O为圆心,以![]() 为半径的圆称为该椭圆的“伴随”.已知椭圆的离心率为
为半径的圆称为该椭圆的“伴随”.已知椭圆的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆C及其“伴随”的方程;
(2)过点![]() 作“伴随”的切线l交椭圆C于A,B两点,记
作“伴随”的切线l交椭圆C于A,B两点,记![]() 为坐标原点)的面积为
为坐标原点)的面积为![]() ,将
,将![]() 表示为m的函数,并求
表示为m的函数,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】条形图给出的是2017年全年及2018年全年全国居民人均可支配收入的平均数与中位数,饼图给出的是2018年全年全国居民人均消费及其构成,现有如下说法:
①2018年全年全国居民人均可支配收入的平均数的增长率低于2017年;
②2018年全年全国居民人均可支配收入的中位数约是平均数的![]() ;
;
③2018年全年全国居民衣(衣着)食(食品烟酒)住(居住)行(交通通信)的支出超过人均消费的![]() .
.
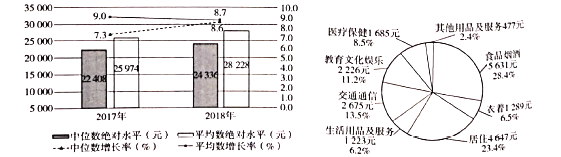
则上述说法中,正确的个数是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是焦距为![]() 的椭圆
的椭圆![]()
![]() 的上、下顶点,P是椭圆上异于顶点的任意一点,直线PA,PB的斜率之积为
的上、下顶点,P是椭圆上异于顶点的任意一点,直线PA,PB的斜率之积为![]() .
.
(1)求椭圆的方程;
(2)若C,D分别是椭圆的左、右顶点,动点M满足![]() ,连接CM交椭圆于点E,试问:x轴上是否存在定点T,使得
,连接CM交椭圆于点E,试问:x轴上是否存在定点T,使得![]() 恒成立?若存在,求出点T坐标,若不存在,请说明理由.
恒成立?若存在,求出点T坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,
两点,![]() 不与
不与![]() 轴垂直,圆
轴垂直,圆![]() .
.
(1)若点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值;
的最大值;
(2)若过线段![]() 的中点
的中点![]() 且垂直于
且垂直于![]() 的直线
的直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为![]() ,且
,且![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)过点![]() 作互相垂直的两条直线,分别交曲线
作互相垂直的两条直线,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() ,若四边形
,若四边形![]() 面积为
面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年在北京召开的国际数学家大会的会标是以我国古代数学家的弦图为基础设计的.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).设其中直角三角形中较小的锐角为![]() ,且
,且![]() ,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
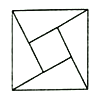
A. 350B. 300C. 250D. 200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com