
����Ŀ��Ϊ���˽����ѧ��Ů�����������ij��ѧ�Գ���Ů�����߽�����һ�β��������������������г���Ƶ�ʷֲ������£�
�� �� | Ƶ�� | Ƶ�� |
145��5��149��5 | 1 | 0��02 |
149��5��153��5 | 4 | 0��08 |
153��5��157��5 | 20 | 0��40 |
157��5��161��5 | 15 | 0��30 |
161��5��165��5 | 8 | 0��16 |
165��5��169��5 | m | n |
�� �� | M | N |
��1���������![]() ����ʾ�����ֱ��Ƕ��٣�
����ʾ�����ֱ��Ƕ��٣�
��2������Ƶ�ʷֲ�ֱ��ͼ��
��3��ȫ��Ů�������������鷶Χ�ڵ�������ࣿ��ֱ��ͼȷ������������λ���Ƕ��٣�
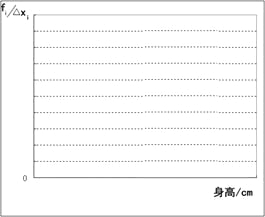
���𰸡���1��0��04,��2���ԣ�3�� ��153��5 ��157��5��Χ�����
�������������������1������Ƶ����Ƶ�ʵ��������������ɵó�M���Ӷ��ó�m;Ƶ��֮�͵���1�ɵ�N��n
��3��Ƶ�ʷֲ�����Ƶ��Խ��ģ����ڸ������������Խ�࣬�������ߵĸ�������ͬ������˵���ߵ�����������ȣ�����ô�����������������λ����
�����������1��![]()
![]()
��2����
��3���ɵڣ�1���ʼ���������֪����![]() ��Χ����ࣨ��Ҳ��ͨ��Ƶ�ʷֲ�ֱ��ͼ�������� �� λ�����ߵ�����������ͬ�������ߵ�����������ȡ���157��5���ߵ��������ʾ�Ϊ0��5��������λ��Ϊ157��5��
��Χ����ࣨ��Ҳ��ͨ��Ƶ�ʷֲ�ֱ��ͼ�������� �� λ�����ߵ�����������ͬ�������ߵ�����������ȡ���157��5���ߵ��������ʾ�Ϊ0��5��������λ��Ϊ157��5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��
��1����![]() ������
������![]() ��ͼ����
��ͼ����![]() �������߷��̣�
�������߷��̣�
��2����![]() �������۷���
�������۷���![]() ��ʵ����ĸ�����
��ʵ����ĸ�����
��3����![]() ʱ�������������
ʱ�������������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������������������
��������������������![]() ��ȡֵ�ļ�����
��ȡֵ�ļ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() ��������������˵�ֱ�ΪA��B��ֱ��
��������������˵�ֱ�ΪA��B��ֱ��![]() ��x�ᡢy��ֱ�������E��F������Բ������C��D��
��x�ᡢy��ֱ�������E��F������Բ������C��D��
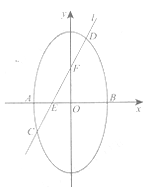
��1����![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����ֱ��AD��CB��б�ʷֱ�Ϊ![]() ����
����![]() ����k��ֵ��
����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͬ�����װ�������ӣ�ÿ��10��.���У���һ��������7���������ĸA��3���������ĸB���ڶ����������к���Ͱ����5�������������������к���8��������2��.���鰴���¹�����У����ڵ�һ�ź�������ȡһ����ȡ�ñ�����ĸA�������ڵڶ��ź�������ȡһ��������һ��ȡ�ñ�����ĸB�������ڵ����ź�������ȡһ����.����ڶ���ȡ�����Ǻ����������ɹ�����ô����ɹ��ĸ���Ϊ�� ��
A.0.59 B.0.54 C.0.8 D.0.15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���㣺��������
���㣺��������![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��1����![]() ����֤��
����֤��![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�
��2����![]() ��
��
�� ������![]() ��ͨ�ʽ��
��ͨ�ʽ��
�� �Ƿ����![]() ��ʹ��
��ʹ��![]() Ϊ����
Ϊ����![]() �е�������ڣ������������������
�е�������ڣ������������������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͬ�����εĵ���ͳ����ʾ���������Ϲ�Ʊ��1000λ��Ʊ�ߵ����䣨��λ���꣩�����ͼ��ʾ.
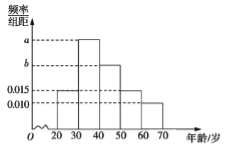
��1����֪�м���������ε����Ϲ�Ʊ�����ɵȲ����У���![]() ��ֵ��
��ֵ��
��2��Ϊ����������Ϲ�Ʊ����ƽ̨�����ù�Ʊ�ͷ��žƵ���ס����ȯ�ķ������д����������������£�
������![]() ���ÿ�˷���20Ԫ����������ε�ÿ�˷���50Ԫ���Ȱ����Ŵ���ȯ�Ľ����÷ֲ�����ķ�ʽ�Ӳ�������1000λ���Ϲ�Ʊ���г�ȡ5�ˣ�������5���������ȡ3�˽��лطõ��飬���3�˻�ô���ȯ�Ľ���ܺ�Ϊ90Ԫ�ĸ���.
���ÿ�˷���20Ԫ����������ε�ÿ�˷���50Ԫ���Ȱ����Ŵ���ȯ�Ľ����÷ֲ�����ķ�ʽ�Ӳ�������1000λ���Ϲ�Ʊ���г�ȡ5�ˣ�������5���������ȡ3�˽��лطõ��飬���3�˻�ô���ȯ�Ľ���ܺ�Ϊ90Ԫ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
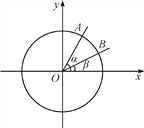
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���Ox��Ϊʼ����������������������ǵ��ձ߷ֱ��뵥λԲ�ཻ��A��B���㣬��֪A��B�ĺ�����ֱ�Ϊ![]() ��
��![]() .��
.��
��1��tan(������)��ֵ��
��2������2���Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x������f��x+y��=f��x��+f��y������x��0ʱ����![]() ����f��1��=��2
����f��1��=��2
��1����f��0����f����1����ֵ��
��2���жϺ���f��x���ĵ����ԣ������ö������֤����
��3����ⲻ��ʽf��2x����f��x2+3x����4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
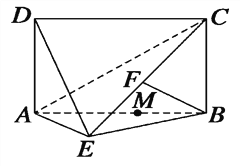
����Ŀ����ͼ���ı���ABCDΪ���Σ�DA��ƽ��ABE��AE��EB��BC��2��
BF��ƽ��ACE���ҵ�F��CE�ϣ�
(1)��֤��AE��BE��
(2)������D��AEC�������
(3)���M���߶�AB�ϣ�������AM��2MB�������߶�CE��ȷ��һ��N��
ʹ��MN��ƽ��DAE.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com