
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©= ![]() Θ§Τδ÷–[x]±μ Ψ≤Μ≥§ΙΐxΒΡΉν¥σ’ϊ ΐΘ°…ηnΓ N* Θ§ Ε®“εΚ· ΐfnΘ®xΘ©ΘΚf1Θ®xΘ©=fΘ®xΘ©Θ§f2Θ®xΘ©=fΘ®f1Θ®xΘ©Θ©Θ§Γ≠Θ§fnΘ®xΘ©=fΘ®fn©¹1Θ®xΘ©Θ©Θ®nΓί2Θ©Θ§‘ρœ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ”– ΔΌy=
Θ§Τδ÷–[x]±μ Ψ≤Μ≥§ΙΐxΒΡΉν¥σ’ϊ ΐΘ°…ηnΓ N* Θ§ Ε®“εΚ· ΐfnΘ®xΘ©ΘΚf1Θ®xΘ©=fΘ®xΘ©Θ§f2Θ®xΘ©=fΘ®f1Θ®xΘ©Θ©Θ§Γ≠Θ§fnΘ®xΘ©=fΘ®fn©¹1Θ®xΘ©Θ©Θ®nΓί2Θ©Θ§‘ρœ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ”– ΔΌy= ![]() ΒΡΕ®“ε”ρΈΣ
ΒΡΕ®“ε”ρΈΣ ![]() ΘΜ
ΘΜ
ΔΎ…ηA={0Θ§1Θ§2}Θ§B={x|f3Θ®xΘ©=xΘ§xΓ A}Θ§‘ρA=BΘΜ
Δέ ![]() ΘΜ
ΘΜ
Δή»τΦ·ΚœM={x|f12Θ®xΘ©=xΘ§xΓ [0Θ§2]}Θ§
‘ρM÷–÷Ν…ΌΚ§”–8Ηω‘ΣΥΊΘ°Θ® Θ©
A.1Ηω
B.2Ηω
C.3Ηω
D.4Ηω
ΓΨ¥πΑΗΓΩC
ΓΨΫβΈωΓΩΫβΘΚΒ±0ΓήxΘΦ1 ±Θ§fΘ®xΘ©=2Θ®1©¹xΘ©ΘΜ Β±1ΓήxΓή2 ±Θ§fΘ®xΘ©=x©¹1Θ°
Φ¥”–fΘ®xΘ©= ![]() Θ§
Θ§
Μ≠≥ωy=fΘ®xΘ©‘Ύ[0Θ§2]ΒΡΆΦœσΘ°
Ε‘”ΎΔΌΘ§Ω…ΒΟfΘ®xΘ©ΓήxΘ§Β±1ΓήxΓή2 ±Θ§x©¹1Γήx≥…ΝΔΘΜ
Β±0ΓήxΘΦ1 ±Θ§2Θ®1©¹xΘ©ΓήxΘ§ΫβΒΟ ![]() ΓήxΘΦ1Θ§Φ¥”–Ε®“ε”ρΈΣ{x|
ΓήxΘΦ1Θ§Φ¥”–Ε®“ε”ρΈΣ{x| ![]() ΓήxΓή2}Θ§
ΓήxΓή2}Θ§
Ι ΔΌ’ΐ»ΖΘΜ
Ε‘”ΎΔΎΘ§Β±x=0 ±Θ§f3Θ®0Θ©=f[f2Θ®0Θ©]=fΘ®fΘ®fΘ®0Θ©Θ©Θ©=fΘ®fΘ®2Θ©Θ©=fΘ®1Θ©=0≥…ΝΔΘΜ
Β±x=1 ±Θ§f3Θ®1Θ©=f[f2Θ®1Θ©]=fΘ®fΘ®fΘ®1Θ©Θ©Θ©=fΘ®fΘ®0Θ©Θ©=fΘ®2Θ©=1≥…ΝΔΘΜ
Β±x=2 ±Θ§f3Θ®2Θ©=f[f2Θ®2Θ©]=fΘ®fΘ®fΘ®2Θ©Θ©Θ©=fΘ®fΘ®1Θ©Θ©=fΘ®0Θ©=2≥…ΝΔΘΜ
Φ¥”–A=BΘ§Ι ΔΎ’ΐ»ΖΘΜ
Ε‘”ΎΔέΘ§f1Θ® ![]() Θ©=2Θ®1©¹
Θ©=2Θ®1©¹ ![]() Θ©=
Θ©= ![]() Θ§f2Θ®
Θ§f2Θ® ![]() Θ©=fΘ®fΘ®
Θ©=fΘ®fΘ® ![]() Θ©Θ©=fΘ®
Θ©Θ©=fΘ® ![]() Θ©=2Θ®1©¹
Θ©=2Θ®1©¹ ![]() Θ©=
Θ©= ![]() Θ§
Θ§
f3Θ® ![]() Θ©=fΘ®f2Θ®
Θ©=fΘ®f2Θ® ![]() Θ©Θ©=fΘ®
Θ©Θ©=fΘ® ![]() Θ©=
Θ©= ![]() ©¹1=
©¹1= ![]() Θ§f4Θ®
Θ§f4Θ® ![]() Θ©=fΘ®f3Θ®
Θ©=fΘ®f3Θ® ![]() Θ©Θ©=fΘ®
Θ©Θ©=fΘ® ![]() Θ©=2Θ®1©¹
Θ©=2Θ®1©¹ ![]() Θ©=
Θ©= ![]() Θ§
Θ§
“ΜΑψΒΊΘ§f4k+rΘ® ![]() Θ©=frΘ®
ȩ=frȮ ![]() ȩȮkȧrà NȩȰ
ȩȮkȧrà NȩȰ
Φ¥”–f2016Θ® ![]() Θ©+f2017Θ®
Θ©+f2017Θ® ![]() Θ©=f4Θ®
Θ©=f4Θ® ![]() Θ©+f1Θ®
Θ©+f1Θ® ![]() Θ©=
Θ©= ![]() +
+ ![]() =
= ![]() Θ§Ι Δέ≤Μ’ΐ»ΖΘΜ
Θ§Ι Δέ≤Μ’ΐ»ΖΘΜ
Ε‘”ΎΔήΘ§”…Θ®1Θ©÷ΣΘ§fΘ® ![]() Θ©=
Θ©= ![]() Θ§ΓύfnΘ®
Θ§ΓύfnΘ® ![]() Θ©=
Θ©= ![]() Θ§‘ρf12Θ®
Θ§‘ρf12Θ® ![]() Θ©=
Θ©= ![]() Θ§Γύ
Θ§Γύ ![]() Γ MΘ°
Γ MΘ°
”…Θ®2Θ©÷ΣΘ§Ε‘x=0ΓΔ1ΓΔ2Θ§Κψ”–f3Θ®xΘ©=xΘ§Γύf12Θ®xΘ©=xΘ§‘ρ0ΓΔ1ΓΔ2Γ MΘ°
”…Θ®3Θ©÷ΣΘ§Ε‘x= ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() Θ§Κψ”–f12Θ®xΘ©=xΘ§Γύ
Θ§Κψ”–f12Θ®xΘ©=xΘ§Γύ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() Γ MΘ°
Γ MΘ°
Ήέ…œΥυ ω ![]() ΓΔ0ΓΔ1ΓΔ2ΓΔ
ΓΔ0ΓΔ1ΓΔ2ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() ΓΔ
ΓΔ ![]() Γ MΘ°
Γ MΘ°
ΓύM÷–÷Ν…ΌΚ§”–8Ηω‘ΣΥΊΘ°Ι Δή’ΐ»ΖΘ°
Ι ―ΓΘΚCΘ°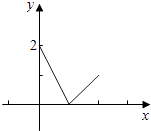


 ΫΧ”ΐ άΦ“Ή¥‘ΣΨμœΒΝ–¥πΑΗ
ΫΧ”ΐ άΦ“Ή¥‘ΣΨμœΒΝ–¥πΑΗ ΜΤΗ‘ΩΈΧΟΉς“Β±ΨœΒΝ–¥πΑΗ
ΜΤΗ‘ΩΈΧΟΉς“Β±ΨœΒΝ–¥πΑΗ ΒΞ‘ΣΦ”ΤΎΡ©Η¥œΑœ»Ζφ¥σΩΦΨμœΒΝ–¥πΑΗ
ΒΞ‘ΣΦ”ΤΎΡ©Η¥œΑœ»Ζφ¥σΩΦΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤CΘΚ![]() Θ®
Θ®![]() Θ©ΒΡάκ–Ρ¬ ΈΣ
Θ©ΒΡάκ–Ρ¬ ΈΣ![]() Θ§«“Ψ≠ΙΐΒψ
Θ§«“Ψ≠ΙΐΒψ![]() Θ§ΥΡ±Ώ–Έ
Θ§ΥΡ±Ώ–Έ![]() ΒΡΥΡΗωΕΞΒψΕΦ‘ΎΆ÷‘≤
ΒΡΥΡΗωΕΞΒψΕΦ‘ΎΆ÷‘≤![]() …œΘ§Ε‘Ϋ«œΏ
…œΘ§Ε‘Ϋ«œΏ![]() Υυ‘Ύ÷±œΏΒΡ–±¬ ΈΣ
Υυ‘Ύ÷±œΏΒΡ–±¬ ΈΣ![]() Θ§«“
Θ§«“![]() Θ§
Θ§![]() .
.
Θ®1Θ©«σΆ÷‘≤CΒΡΖΫ≥ΧΘΜ
Θ®2Θ©«σΥΡ±Ώ–Έ![]() ΟφΜΐΒΡΉν¥σ÷Β.
ΟφΜΐΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΙΊ”Ύ”Ο–±Εΰ≤βΜ≠Ζ®Μ≠÷±ΙέΆΦΒΡΥΒΖ®÷–Θ§¥μΈσΒΡ «Θ® Θ©
A. ”Ο–±Εΰ≤βΜ≠Ζ®Μ≠≥ωΒΡ÷±ΙέΆΦ «‘ΎΤΫ––ΆΕ”Αœ¬Μ≠≥ωΒΡΩ’ΦδΆΦ–Έ
B. ΦΗΚΈΧεΒΡ÷±ΙέΆΦΒΡ≥ΛΓΔΩμΓΔΗΏ”κΤδΦΗΚΈΧεΒΡ≥ΛΓΔΩμΓΔΗΏΒΡ±»άΐœύΆ§
C. Υ°ΤΫΖ≈÷ΟΒΡΨΊ–ΈΒΡ÷±ΙέΆΦ «ΤΫ––ΥΡ±Ώ–Έ
D. Υ°ΤΫΖ≈÷ΟΒΡ‘≤ΒΡ÷±ΙέΆΦ «Ά÷‘≤
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ¥”“Μ≈ζη÷Ή”÷–Θ§ΥφΜζ≥ι»Γ100ΗωΘ§ΜώΒΟΤδ÷ΊΝΩΘ®ΒΞΈΜΘΚΩΥΘ© ΐΨίΑ¥’’«χΦδ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ϋχ––Ζ÷ΉιΘ§ΒΟΒΫΗ≈¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ Ψ.
Ϋχ––Ζ÷ΉιΘ§ΒΟΒΫΗ≈¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ Ψ.
Θ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΦΤΥψ≥ι»ΓΒΡ100Ηωη÷Ή”ΒΡ÷ΊΝΩ÷Ύ ΐΒΡΙάΦΤ÷Β.
Θ®2Θ©”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”÷ΊΝΩ‘Ύ![]() ΚΆ
ΚΆ![]() ΒΡη÷Ή”÷–Ι≤≥ι»Γ5ΗωΘ§Τδ÷–÷ΊΝΩ‘Ύ
ΒΡη÷Ή”÷–Ι≤≥ι»Γ5ΗωΘ§Τδ÷–÷ΊΝΩ‘Ύ![]() ΒΡ”–ΦΗΗωΘΩ
ΒΡ”–ΦΗΗωΘΩ
Θ®3Θ©‘ΎΘ®2Θ©÷–≥ι≥ωΒΡ5Ηωη÷Ή”÷–Θ§»Έ»Γ2»ΥΘ§«σ÷ΊΝΩ‘Ύ![]() ΒΡη÷Ή”ΉνΕύ”–1ΗωΒΡΗ≈¬ .
ΒΡη÷Ή”ΉνΕύ”–1ΗωΒΡΗ≈¬ .

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕ·Βψ P ”κΕ®Βψ![]() ΒΡΨύάκΚΆΥϋΒΫΕ®÷±œΏ x 4 ΒΡΨύάκΒΡ±» «1: 2 Θ§Φ«Ε·Βψ P ΒΡΙλΦΘΈΣ«ζœΏ EΘ°
ΒΡΨύάκΚΆΥϋΒΫΕ®÷±œΏ x 4 ΒΡΨύάκΒΡ±» «1: 2 Θ§Φ«Ε·Βψ P ΒΡΙλΦΘΈΣ«ζœΏ EΘ°
Θ®1Θ©«σ«ζœΏ E ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η A ««ζœΏ E …œΒΡ“ΜΗωΒψΘ§÷±œΏ AF ΫΜ«ζœΏ E ”ΎΝμ“ΜΒψ BΘ§“‘ AB ΈΣ±ΏΉς“ΜΗωΤΫ––ΥΡ±Ώ–ΈΘ§ΕΞΒψ AΓΔBΓΔCΓΔD ΕΦ‘ΎΙλΦΘ E …œΘ§≈–ΕœΤΫ––ΥΡ±Ώ–Έ ABCD ΡήΖώΈΣΝβ–ΈΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®3Θ©Β±ΤΫ––ΥΡ±Ώ–Έ ABCD ΒΡΟφΜΐ»ΓΒΫΉν¥σ÷Β ±Θ§≈–ΕœΥϋΒΡ–ΈΉ¥Θ§≤Δ«σ≥ωΤδΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ![]() Ρξ
Ρξ![]() ‘¬
‘¬![]() »’Θ§ΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±‘Ύ…ΫΕΪ«ύΒΚΩΣΡΜ.ΈΣΝΥΫβΡΡ–©»ΥΗϋΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±Θ§Ρ≥ΜζΙΙΥφΜζ≥ι»ΓΝΥΡξΝδ‘Ύ
»’Θ§ΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±‘Ύ…ΫΕΪ«ύΒΚΩΣΡΜ.ΈΣΝΥΫβΡΡ–©»ΥΗϋΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±Θ§Ρ≥ΜζΙΙΥφΜζ≥ι»ΓΝΥΡξΝδ‘Ύ![]() -
-![]() Υξ÷°ΦδΒΡ
Υξ÷°ΦδΒΡ![]() »ΥΫχ––Βς≤ιΘ§≤ΔΑ¥ΡξΝδΜφ÷Τ≥…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ ΨΘ§ΤδΖ÷Ήι«χΦδΈΣΘΚ
»ΥΫχ––Βς≤ιΘ§≤ΔΑ¥ΡξΝδΜφ÷Τ≥…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ ΨΘ§ΤδΖ÷Ήι«χΦδΈΣΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .Α―ΡξΝδ¬δ‘Ύ«χΦδ
.Α―ΡξΝδ¬δ‘Ύ«χΦδ![]() ΚΆ
ΚΆ![]() ΡΎΒΡ»ΥΖ÷±π≥ΤΈΣΓΑ«ύ…ΌΡξΓ±ΚΆΓΑ÷–άœΡξΓ±.
ΡΎΒΡ»ΥΖ÷±π≥ΤΈΣΓΑ«ύ…ΌΡξΓ±ΚΆΓΑ÷–άœΡξΓ±.

ΙΊΉΔ | ≤ΜΙΊΉΔ | ΚœΦΤ | |
«ύ…ΌΡξ |
| ||
÷–άœΡξ | |||
ΚœΦΤ |
|
|
|
Θ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ«σ―υ±ΨΒΡ÷–ΈΜ ΐΘ®±ΘΝτΝΫΈΜ–Γ ΐΘ©ΚΆ÷Ύ ΐΘΜ
Θ®2Θ©ΗυΨί“―÷ΣΧθΦΰΆξ≥…![]() Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ”–
Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ”–![]() ΒΡΑ―Έ’»œΈΣΓΑ÷–άœΡξΓ±±»ΓΑ«ύ…ΌΡξΓ±ΗϋΦ”ΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±ΘΜ
ΒΡΑ―Έ’»œΈΣΓΑ÷–άœΡξΓ±±»ΓΑ«ύ…ΌΡξΓ±ΗϋΦ”ΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±ΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§![]() Θ®
Θ®![]() Θ§
Θ§![]() «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©.
«Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©.
Θ®1Θ©«σΚ· ΐ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©»τ![]() Θ§Β±
Θ§Β±![]() ±Θ§«σΚ· ΐ
±Θ§«σΚ· ΐ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©»τ![]() Θ§«“
Θ§«“![]() Θ§±»ΫœΘΚ
Θ§±»ΫœΘΚ![]() ”κ
”κ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–{an}ΒΡ«ΑnœνΚΆΈΣSn Θ§ «“¬ζΉψ4nSn=Θ®n+1Θ©2anΘ®nΓ N*Θ©Θ°a1=1
Θ®ΔώΘ©«σanΘΜ
Θ®ΔρΘ©…ηbn= ![]() Θ§ ΐΝ–{bn}ΒΡ«ΑnœνΚΆΈΣTn Θ§ «σ÷ΛΘΚTn
Θ§ ΐΝ–{bn}ΒΡ«ΑnœνΚΆΈΣTn Θ§ «σ÷ΛΘΚTn ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ![]() Θ§“―÷ΣΒΪ
Θ§“―÷ΣΒΪ![]() ‘ΎΆ÷‘≤
‘ΎΆ÷‘≤![]() …œ.
…œ.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©Ιΐ”“ΫΙΒψ![]() Ής–±¬ ΈΣΒΡ÷±œΏ
Ής–±¬ ΈΣΒΡ÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§‘Ύ
ΝΫΒψΘ§‘Ύ![]() ÷α…œ «Ζώ¥φ‘ΎΒψ
÷α…œ «Ζώ¥φ‘ΎΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() ≥…ΝΔΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ω
≥…ΝΔΘΩ»γΙϊ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ»Γ÷ΒΖΕΈßΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com