
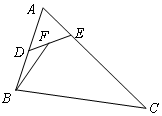
 如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,
如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,分析 (1)用$\overrightarrow{AD}$,$\overrightarrow{AE}$表示出$\overrightarrow{AF}$,即可得出结论;
(2)用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{EF}$,再计算$\overrightarrow{BA}$•$\overrightarrow{EF}$.
解答 解:(1)∵$\overrightarrow{BF}$=-$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{AC}$,∴$\overrightarrow{AF}$=$\overrightarrow{BF}-\overrightarrow{BA}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{AC}$,
又$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,∴$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$+$\frac{1}{2}$$\overrightarrow{AE}$,
∴F为DE的中点.
(2)由(1)可得$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{ED}$=$\frac{1}{2}$($\overrightarrow{AD}-\overrightarrow{AE}$),
∵$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,∴$\overrightarrow{EF}$=$\frac{1}{4}$$\overrightarrow{AB}$-$\frac{1}{10}$$\overrightarrow{AC}$.
∴$\overrightarrow{BA}•\overrightarrow{EF}$=-$\overrightarrow{AB}$•($\frac{1}{4}$$\overrightarrow{AB}$-$\frac{1}{10}$$\overrightarrow{AC}$)=-$\frac{1}{4}$${\overrightarrow{AB}}^{2}$+$\frac{1}{10}$$\overrightarrow{AB}•\overrightarrow{AC}$
=-$\frac{1}{4}$×4+$\frac{1}{10}$×2×6×cos60°=-$\frac{2}{5}$.
点评 本题考查了平面向量的基本定理,平面向量的数量积运算,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在六面体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1.
如图,在六面体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,平面ABCD⊥平面A1B1BA,平面ABCD平面B1BCC1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (0,2) | C. | [-2,2] | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
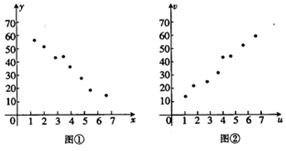 对变量x,y有观测数据(xi,yi)(i=1,2,3,…,8),得散点图如图①所示,对变量u,v有观测数据(ui,vi)(i=1,2,3,…,8),得散点图如图②所示,由这两个散点图可以判断( )
对变量x,y有观测数据(xi,yi)(i=1,2,3,…,8),得散点图如图①所示,对变量u,v有观测数据(ui,vi)(i=1,2,3,…,8),得散点图如图②所示,由这两个散点图可以判断( )| A. | 变量x与y正相关;u与v正相关 | B. | 变量x与y正相关;u与v负相关 | ||
| C. | 变量x与y负相关;u与v正相关 | D. | 变量x与y负相关;u与v负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,面积为10的矩形中有一封闭曲线围成的阴影区域,在矩形中随机撒一粒种子,它落在阴影区域内的概率为$\frac{3}{5}$,则阴影区域的面积为6.
如图,面积为10的矩形中有一封闭曲线围成的阴影区域,在矩形中随机撒一粒种子,它落在阴影区域内的概率为$\frac{3}{5}$,则阴影区域的面积为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-2,0) | C. | (1,2) | D. | (-2,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com