
【题目】某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
【答案】
(1)解:根据所给的数据,写出5组坐标,作出散点图如图所示:
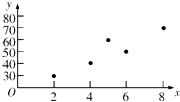
(2)解:求回归直线方程.
![]()
![]() =50
=50
b= ![]() =
= ![]()
a=50﹣6.5×5=17.5
∴因此回归直线方程为y=6.5x+17.5
(3)解:当x=12时,预报y的值为y=12×6.5+17.5=95.5万元.
即广告费用为12万元时,销售收入y的值大约是95.5万元
【解析】(1)根据所给的数据,写出5组坐标,作出散点图如图所示.(2)根据所给的数据先做出横标和纵标的平均数,利用最小二乘法写出线性回归方程系数的表达式,把样本中心点代入求出a的值,得到线性回归方程.(3)根据所给的变量x的值,把值代入线性回归方程,得到对应的y的值,这里的y的值是一个预报值.


科目:高中数学 来源: 题型:
【题目】若 ![]() ,
, ![]() ,
, ![]() 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足 ![]() +
+ ![]() +
+ ![]() =
= ![]() ,且向量
,且向量 ![]() =x
=x ![]() +
+ ![]()
![]() +(x+
+(x+ ![]() )
) ![]() (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求 ![]() 与
与 ![]() 所成角的大小;
所成角的大小;
(2)记f(x)=| ![]() |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥S﹣ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC所成的角是( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b﹣1(a≠0).
(1)当a=1,b=﹣2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+ ![]() 对称,求b的最小值.
对称,求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在x轴上的椭圆,离心率为 ![]() 且过点(
且过点( ![]() ,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
(1)若线段AB中点的横坐标是﹣ ![]() ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使 ![]() 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)已知![]() 为实数,函数
为实数,函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,令
时,令![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)当![]() 时,令
时,令![]() ,是否存在实数
,是否存在实数![]() ,使得对于函数
,使得对于函数![]() 定义域中的任意实数
定义域中的任意实数![]() ,均存在实数
,均存在实数![]() ,有
,有![]() 成立,若存在,求出实数
成立,若存在,求出实数![]() 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).
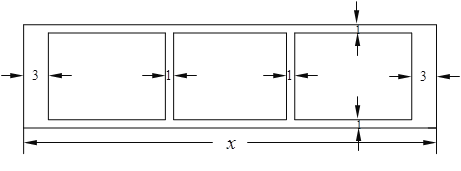
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)如图,我市有一个健身公园,由一个直径为2km的半圆和一个以![]() 为斜边的等腰直角三角形
为斜边的等腰直角三角形![]() 构成,其中
构成,其中![]() 为
为![]() 的中点.现准备在公园里建设一条四边形健康跑道
的中点.现准备在公园里建设一条四边形健康跑道![]() ,按实际需要,四边形
,按实际需要,四边形![]() 的两个顶点
的两个顶点![]() 分别在线段
分别在线段![]() 上,另外两个顶点
上,另外两个顶点![]() 在半圆上,
在半圆上, ![]() ,且
,且![]() 间的距离为1km.设四边形
间的距离为1km.设四边形![]() 的周长为
的周长为![]() km.
km.

(1)若![]() 分别为
分别为![]() 的中点,求
的中点,求![]() 长;
长;
(2)求周长![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com