
【题目】已知在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为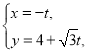 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线和曲线
分别交直线和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
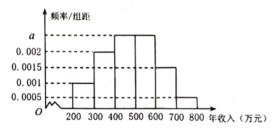
①样本数据落在区间![]() 的频率为0.45;
的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待工作的态度进行了调查,统计数据如下所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法有多大把握认为学生的学习积极性与对班级工作的态度有关系?并说明理由.
本题参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
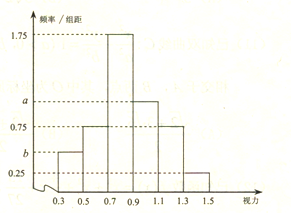
【题目】从某校高三年级中随机抽取100名学生,对其高校招生体检表中的视图情况进行统计,得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若某大学![]() 专业的报考要求之一是视力在0.9以上,则对这100人中能报考
专业的报考要求之一是视力在0.9以上,则对这100人中能报考![]() 专业的学生采用按视力分层抽样的方法抽取8人,调查他们对
专业的学生采用按视力分层抽样的方法抽取8人,调查他们对![]() 专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学
专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学![]() 专业的调查,记抽到的学生中视力在
专业的调查,记抽到的学生中视力在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线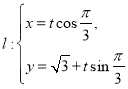 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题,其中正确的是( )
A.对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,“
越小,“![]() 与
与![]() 有关系”可信程度越大
有关系”可信程度越大
B.残差点比较均匀地落在水平带状区域内,带状区域越窄,则模型拟合精度越高
C.相关指数![]() 越小,则残差平方和越大,模型的拟合效果越好
越小,则残差平方和越大,模型的拟合效果越好
D.两个随机变量相关性越强,则相关系数的绝对值越接近![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() 。
。
(1)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)求乙至多击目标2次的概率;
(3)求甲恰好比乙多击中目标2次的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
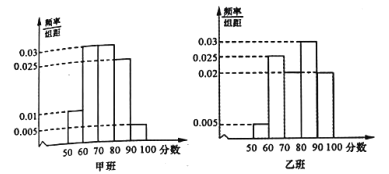
【题目】为了响应党的十九大所提出的教育教学改革,某校启动了数学教学方法的探索,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班40人,甲班按原有传统模式教学,乙班实施自主学习模式.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
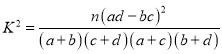
(1)完成表格,并判断是否有![]() 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 合计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
合计 |
(2)从乙班![]() ,
,![]() ,
,![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com