
【题目】某工厂![]() ,
,![]() 两条相互独立的生产线生产同款产品,在产量一样的情况下,通过日常监控得知,
两条相互独立的生产线生产同款产品,在产量一样的情况下,通过日常监控得知,![]() ,
,![]() 生产线生产的产品为合格品的概率分别为
生产线生产的产品为合格品的概率分别为![]() 和
和![]() .
.
(1)从![]() ,
,![]() 生产线上各抽检一件产品,若使得产品至少有一件合格的概率不低于99.5%,求
生产线上各抽检一件产品,若使得产品至少有一件合格的概率不低于99.5%,求![]() 的最小值
的最小值![]() ;
;
(2)假设不合格的产品均可进行返工修复为合格品,以(1)中确定的![]() 作为
作为![]() 的值.
的值.
①已知![]() ,
,![]() 生产线的不合格品返工后每件产品可分别挽回损失5元和3元,若从两条生产线上各随机抽检1000件产品,以挽回损失的平均数为判断依据,估计哪条生产线的挽回损失较多?
生产线的不合格品返工后每件产品可分别挽回损失5元和3元,若从两条生产线上各随机抽检1000件产品,以挽回损失的平均数为判断依据,估计哪条生产线的挽回损失较多?
②若最终的合格品(包括返工修复后的合格品)按照一、二、三等级分类后,每件可分别获利10元、8元、6元,现从![]() ,
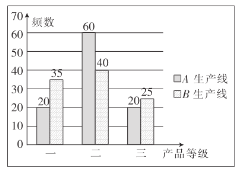
,![]() 生产线的最终合格品中各随机抽取100件进行分级检测,结果统计如图所示,用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为
生产线的最终合格品中各随机抽取100件进行分级检测,结果统计如图所示,用样本的频率分布估计总体分布,记该工厂生产一件产品的利润为![]() ,求
,求![]() 的分布列并估计该厂产量2000件时利润的期望值.
的分布列并估计该厂产量2000件时利润的期望值.
【答案】(1)0.95;(2)①![]() 生产线挽回的平均损失较多;②分布列见解析,16200元.
生产线挽回的平均损失较多;②分布列见解析,16200元.
【解析】
(1)根据独立事件同时发生以及对立事件的概率,求出产品至少有一件合格的概率,根据已知建立![]() 的不等量关系,即可求解;
的不等量关系,即可求解;
(2)①根据(1)的结论求出![]() 生产线不合格品率,进而求出两条生产线的不合格品数,即可求出结论;
生产线不合格品率,进而求出两条生产线的不合格品数,即可求出结论;
②![]() 的可能取值为6,8,10,根据频数分布图,求出
的可能取值为6,8,10,根据频数分布图,求出![]() 可能值的频率,得到
可能值的频率,得到![]() 的分布列,根据期望公式求解即可.
的分布列,根据期望公式求解即可.
(1)设从![]() ,
,![]() 生产线上各抽检一件产品,至少有一件合格为事件
生产线上各抽检一件产品,至少有一件合格为事件![]() ,从
,从![]() ,
,![]() 生产线上抽检到合格品分别为事件
生产线上抽检到合格品分别为事件![]() ,
,![]() ,由题知,
,由题知,![]() ,
,![]() 互为独立事件,所以
互为独立事件,所以![]() ,
,![]() ,
,
![]()
![]() ,
,
令![]() ,解得
,解得![]() ,故
,故![]() 的最小值
的最小值![]() .
.
(2)由(1)可知,![]() ,
,![]() 生产线生产的产品为合格品率分别为0.95和0.9,
生产线生产的产品为合格品率分别为0.95和0.9,
不合格品率分别为0.05和0.1.
①由题知,![]() 生产线上随机抽检1000件产品,
生产线上随机抽检1000件产品,
估计不合格品![]() (件),
(件),
可挽回损失为![]() (元),
(元),
![]() 生产线上随机抽检1000件产品,
生产线上随机抽检1000件产品,
估计不合格品![]() (件),
(件),
可挽回损失为![]() (元).
(元).
由此,估计![]() 生产线挽回的平均损失较多.
生产线挽回的平均损失较多.
②由题知,![]() 的所有可能取值为6,8,10,
的所有可能取值为6,8,10,
用样本的频率分布估计总体分布,则
![]() ,
,![]() ,
,
![]() ,
,
所以![]() 的分布列为
的分布列为
| 6 | 8 | 10 |
|
|
|
|
所以![]() (元).
(元).
故估计该厂产量为2000件时利润的期望值为![]() (元).
(元).


科目:高中数学 来源: 题型:
【题目】设数列![]() 对任意
对任意![]() 都有
都有![]() (其中
(其中![]() 、
、![]() 、
、![]() 是常数) .
是常数) .
(Ⅰ)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ;
;
(Ⅱ)当![]() ,
,![]() ,
,![]() 时,若
时,若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若数列![]() 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.当![]() ,
,![]() ,
,![]() 时,设
时,设![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,试问:是否存在这样的“封闭数列”,使得对任意
,试问:是否存在这样的“封闭数列”,使得对任意![]() ,都有
,都有![]() ,且
,且![]() .若存在,求数列
.若存在,求数列![]() 的首项
的首项![]() 的所有取值;若不存在,说明理由.
的所有取值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中一定正确的是( )
(注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生).

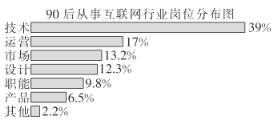
A.互联网行业从业人员中80前占3%以上
B.互联网行业90后中,从事设计岗位的人数比从事市场岗位的人数要多
C.互联网行业中从事技术岗位的人数超过总人数的20%
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在定义域
在定义域![]() 内的某个区间
内的某个区间![]() 上是增函数,且
上是增函数,且![]() 在
在![]() 上也是增函数,则称
上也是增函数,则称![]() 是
是![]() 上的“完美增函数”.已知
上的“完美增函数”.已知![]() ,
,![]() .
.
(1)判断函数![]() 是否为区间
是否为区间![]() 上的“完美增函数”;
上的“完美增函数”;
(2)若函数![]() 是区间
是区间![]() 上的“完美增函数”,求实数
上的“完美增函数”,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,图中直棱柱![]() 的底面是菱形,其中
的底面是菱形,其中![]() .又点
.又点![]() 分别在棱
分别在棱![]() 上运动,且满足:
上运动,且满足:![]() ,
,![]() .
.
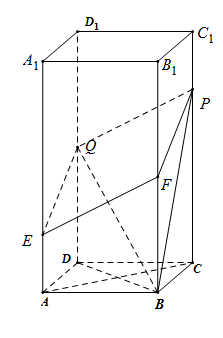
(1)求证:![]() 四点共面,并证明
四点共面,并证明![]() ∥平面
∥平面![]() .
.
(2)是否存在点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ?如果存在,求出
?如果存在,求出![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”经统计“青少年人”和“中老年人”的人数之比为
内的人分别称为“青少年人”和“中老年人”经统计“青少年人”和“中老年人”的人数之比为![]() .其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是
.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是![]() .
.

(1)求图中![]() 的值;现釆用分层抽样在
的值;现釆用分层抽样在![]() 和
和![]() 中随机抽取8名代表,从8人中仼选2人,求2人中至少有1个是“中老年人”的概率是多少?
中随机抽取8名代表,从8人中仼选2人,求2人中至少有1个是“中老年人”的概率是多少?
(2)根据已知条件,完成下面的![]() 列联表,并根据此统计结果判断:能否有
列联表,并根据此统计结果判断:能否有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”?
的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
参考数据及公式:
| 0.150 | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com