
【题目】如图,已知抛物线![]() 的顶点在坐标原点,焦点在x轴上,且过点(2,4),圆
的顶点在坐标原点,焦点在x轴上,且过点(2,4),圆![]() ,过圆心
,过圆心![]() 的直线l与抛物线和圆分别交于P,Q,M,N,则
的直线l与抛物线和圆分别交于P,Q,M,N,则![]() 的最小值为________.
的最小值为________.

【答案】42
【解析】
设抛物线的标准方程,将点代入抛物线方程,求得抛物线方程,由抛物线的焦点弦性质,求得![]() ,根据抛物线的性质及基本不等式,即可求得答案.
,根据抛物线的性质及基本不等式,即可求得答案.
设抛物线的方程:y2=2px(p>0),则16=2p×2,则2p=8,
∴抛物线的标准方程:y2=8x,焦点坐标F(2,0),
由直线PQ过抛物线的焦点,则![]() ,
,
圆C2:(x﹣2)2+y2=1圆心为(2,0),半径1,
|PN|+9|QM|=|PF|+1+9(|QF|+1)
=|PF|+9|QF|+10=2(|PF|+9|QF|)×(![]() )+10
)+10
=2(10![]() )+10≥2(10+2
)+10≥2(10+2![]() )+10=42,
)+10=42,
∴|PN|+9|QM|的最小值为42,
故答案为42.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x-x2)ex-1.
(1)求函数f(x)的单调区间;
(2)若对任意x≥1,都有f(x)-mx-1+m≤0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,得到如图的频率分布直方图(图1).

(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到图2中数据,根据表中的数据,能否在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一次骰子,将得到的点数分别记为![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市创业园区新引进一家生产环保产品的公司,已知该环保产品每售出1盒的利润为0.3万元,当月未售出的环保产品,每盒亏损0.12万元.根据统计资料,该环保产品的市场月需求量的频率分布直方图如图所示.
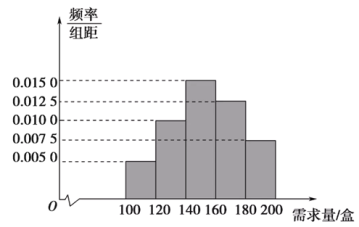
(1)若该环保产品的月进货量为160盒,以![]() (单位:盒,
(单位:盒,![]() )表示该产品一个月内的市场需求量,
)表示该产品一个月内的市场需求量,![]() (单位:万元)表示该公司生产该环保产品的月利润.
(单位:万元)表示该公司生产该环保产品的月利润.
①将![]() 表示为
表示为![]() 的函数;
的函数;
②根据频率分布直方图估计利润![]() 不少于39.6万元的概率.
不少于39.6万元的概率.
(2)在频率分布直方图的月需求量分组中,以各组的区间中点值代表该组的月需求量,当月进货量为158箱时,写出月利润![]() (单位:万元)的所有可能值.
(单位:万元)的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)若抛物线![]() 的焦点到准线的距离为4,直线
的焦点到准线的距离为4,直线![]() ,求直线
,求直线![]() 截抛物线
截抛物线![]() 所得的弦长;
所得的弦长;
(2)过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,过点
两点,过点![]() 作抛物线的切线,两切线相交于点
作抛物线的切线,两切线相交于点![]() ,若
,若![]() 分别表示直线
分别表示直线![]() 与直线
与直线![]() 的斜率,且
的斜率,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com