练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数被称为狄利克雷函数，其中为实数集，为有理数集，则关于函数有如下四个命题：①；②函数是偶函数；③任取一个不为零的有理数，对任意的恒成立；④存在三个点，，，使得为等边三角形.其中真命题的个数有（ ）

    A.1个B.2个C.3个D.4个

    【答案】D

    【解析】

    根据所给的定义，运用分类讨论的方法、取特殊值法进行逐一判断即可.

    ①∵当为有理数时，；当为无理数时，，

    ∴当为有理数时，；

    当为无理数时，，

    即不管是有理数还是无理数，均有，故①正确；

    ②∵有理数的相反数还是有理数，无理数的相反数还是无理数，

    ∴对任意，都有，故②正确；

    ③若是有理数，则也是有理数； 若是无理数，则也是无理数，

    ∴根据函数的表达式，任取一个不为零的有理数，对恒成立，故③正确；

    ④取，，，可得，，，

    ∴，，，恰好为等边三角形，故④正确.

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中），且曲线在点处的切线垂直于直线.

    （1）求的值及此时的切线方程；

    （2）求函数的单调区间与极值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若，，求的值域；

    （2）当时，求的最小值；

    （3）是否存在实数、，同时满足下列条件：① ；② 当的定义域为时，其值域为．若存在，求出、的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电子产品生产企业生产一种产品，原计划每天可以生产吨产品，每吨产品可以获得净利润万元，其中，由于受市场低迷的影响，该企业的净利润出现较大幅度下滑．为提升利润，该企业决定每天投入20万元作为奖金刺激生产．在此方案影响下预计每天可增产吨产品，但是受原材料数量限制，增产量不会超过原计划每天产量的四分之一．试求在每天投入20万元奖金的情况下，该企业每天至少可获得多少利润(假定每天生产出来的产品都能销售出去)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若定义在D上的函数f（x）满足：对任意x∈D，存在常数M>0，都有-M<f（x）<M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界。

    （Ⅰ）判断函数f（x）=-2x+2，x∈[0，2]是否是有界函数，请说明理由；

    （Ⅱ）若函数f（x）=1++，x∈[0，+∞）是以3为上界的有界函数，求实数a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某兴趣小组有男生20人，女生10人，从中抽取一个容量为5的样本，恰好抽到2名男生和3名女生，则

    ①该抽样可能是系统抽样；

    ②该抽样可能是随机抽样：

    ③该抽样一定不是分层抽样；

    ④本次抽样中每个人被抽到的概率都是．

    其中说法正确的为（ ）

    A.①②③B.②③C.②③④D.③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据以往的经验，某建筑工程施工期间的降水量（单位：）对工期的影响如下表：

    根据某气象站的资料，某调查小组抄录了该工程施工地某月前20天的降水量的数据，绘制得到降水量的折线图，如下图所示.

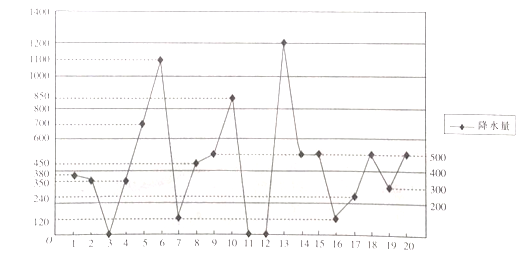
    （1）求这20天的平均降水量；

    （2）根据降水量的折线图，分别估计该工程施工延误天数的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数集(,)具有性质P;对任意的i,j(),与两数中至少有一个属于A.

    (1)分别判断数集与是否具有性质P,并说明理由;

    (2)证明:,且;

    (3)当时,若,求集合A.

    查看答案和解析>>

    同步练习册答案