
【题目】携号转网,也称作号码携带、移机不改号,即无需改变自己的手机号码,就能转换运营商,并享受其提供的各种服务.2019年11月27日,工信部宣布携号转网在全国范围正式启动.某运营商为提质量保客户,从运营系统中选出300名客户,对业务水平和服务水平的评价进行统计,其中业务水平的满意率为![]() ,服务水平的满意率为
,服务水平的满意率为![]() ,对业务水平和服务水平都满意的客户有180人.
,对业务水平和服务水平都满意的客户有180人.
(Ⅰ)完成下面![]() 列联表,并分析是否有
列联表,并分析是否有![]() 的把握认为业务水平与服务水平有关;
的把握认为业务水平与服务水平有关;
对服务水平满意人数 | 对服务水平不满意人数 | 合计 | |
对业务水平满意人数 | |||
对业务水平不满意人数 | |||
合计 |
(Ⅱ)为进一步提高服务质量,在选出的对服务水平不满意的客户中,抽取2名征求改进意见,用![]() 表示对业务水平不满意的人数,求
表示对业务水平不满意的人数,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)若用频率代替概率,假定在业务服务协议终止时,对业务水平和服务水平两项都满意的客户流失率为![]() ,只对其中一项不满意的客户流失率为
,只对其中一项不满意的客户流失率为![]() ,对两项都不满意的客户流失率为
,对两项都不满意的客户流失率为![]() ,从该运营系统中任选4名客户,则在业务服务协议终止时至少有2名客户流失的概率为多少?
,从该运营系统中任选4名客户,则在业务服务协议终止时至少有2名客户流失的概率为多少?
附: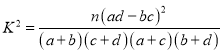 ,
,![]() .
.
0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(Ⅰ)列联表详见解析,有![]() 的把握认为业务水平满意与服务水平满意有关;(Ⅱ)分布列详见解析,期望为
的把握认为业务水平满意与服务水平满意有关;(Ⅱ)分布列详见解析,期望为![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)根据所给数据列表,计算![]() 后比较临界值即可得出结论;
后比较临界值即可得出结论;
(Ⅱ)根据超几何分布得出随机变量的概率,列出分布列求期望即可;
(Ⅲ)由互斥事件和的概率公式计算运营系统中任选一名客户流失的概率![]() ,从运营系统中任选4名客户流失人数服从二项分布
,从运营系统中任选4名客户流失人数服从二项分布![]() ,根据二项分布求解即可.
,根据二项分布求解即可.
(Ⅰ)由题意知对业务满意的有260人,对服务不满意的有100人,得![]() 列联表
列联表
对服务水平满意人数 | 对服务水平不满意人数 | 合计 | |
对业务水平满意人数 | 180 | 80 | 260 |
对业务水平不满意人数 | 20 | 20 | 40 |
合计 | 200 | 100 | 300 |
经计算得![]() ,
,
所以有![]() 的把握认为业务水平满意与服务水平满意有关.
的把握认为业务水平满意与服务水平满意有关.
(Ⅱ)![]() 的可能值为0,1,2.
的可能值为0,1,2.
则![]() ,
,![]() ,
,![]() ,
,
| 0 | 1 | 2 |
|
|
|
|
![]() .
.
(Ⅲ)在业务服务协议终止时,对业务水平和服务水平都满意的客户流失的概率为![]() ,只有一项满意的客户流失的概率为
,只有一项满意的客户流失的概率为![]() ,对二者都不满意的客户流失的概率为
,对二者都不满意的客户流失的概率为![]() .
.
所以从运营系统中任选一名客户流失的概率为![]() ,
,
故在业务服务协议终止时,从运营系统中任选4名客户,至少有2名客户流失的概率为
![]() .
.


科目:高中数学 来源: 题型:
【题目】随着社会的发展与进步,传播和存储状态已全面进入数字时代,以数字格式存储,以互联网为平台进行传输的音乐——数字音乐已然融入了我们的日常生活.虽然我国音乐相关市场仍处在起步阶段,但政策利好使音乐产业逐渐得到资本市场更多的关注.对比如下两幅统计图,下列说法正确的是( )
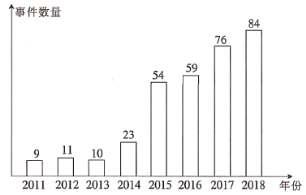
2011-2018年中国音乐产业投融资事件数量统计图
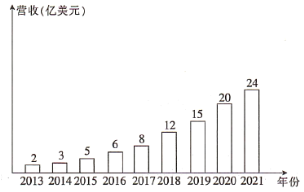
2013-2021年中国录制音乐营收变化及趋势预测统计图
A.2011~2018年我国音乐产业投融资事件数量逐年增长
B.2013~2018年我国录制音乐营收与音乐产业投融资事件数量呈正相关关系
C.2016年我国音乐产业投融资事件的平均营收约为![]() 亿美元
亿美元
D.2013~2019年我国录制音乐营收年增长率最大的是2018年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数![]() ,使对任意的
,使对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为
为![]() 数列.
数列.
(1)已知![]() 是公差为2的等差数列,其前n项和为
是公差为2的等差数列,其前n项和为![]() .若
.若![]() 是
是![]() 数列,求
数列,求![]() 的取值范围;
的取值范围;
(2)已知数列![]() 的各项均为正数,记数列
的各项均为正数,记数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
①求证:数列![]() 是等比数列;
是等比数列;
②设![]() ,试证明:存在常数
,试证明:存在常数![]() ,对于任意的
,对于任意的![]() ,数列
,数列![]() 都是
都是![]() 数列.
数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济结构调整和方式转变,社会对高质量人才的需求越来越大,因此考研现象在我国不断升温.某大学一学院甲、乙两个本科专业,研究生的报考和录取情况如下表,则
性别 | 甲专业报考人数 | 乙专业报考人数 | 性别 | 甲专业录取率 | 乙专业录取率 | |
男 | 100 | 400 | 男 |
|
| |
女 | 300 | 100 | 女 |
|
|
A.甲专业比乙专业的录取率高B.乙专业比甲专业的录取率高
C.男生比女生的录取率高D.女生比男生的录取率高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.已知a2+c2=b2![]() ac.
ac.
(1)求cosB及tan2B的值;
(2)若b=3,A![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆柱![]() 中,AB为圆
中,AB为圆![]() 的直径,
的直径,![]() 是
是![]() 的两个三等分点,EA,FC,GB都是圆柱
的两个三等分点,EA,FC,GB都是圆柱![]() 的母线.
的母线.
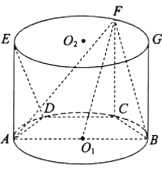
(1)求证:![]() 平面ADE;
平面ADE;
(2)设BC=1,已知直线AF与平面ACB所成的角为30°,求二面角A—FB—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
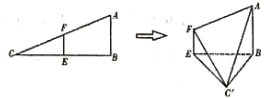
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com