
当一个非空数集 满足条件“如果
满足条件“如果 则
则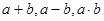
 ,并且当
,并且当 时,
时, ”时,我们就称
”时,我们就称 为一个数域.以下四个关于数域命题:①
为一个数域.以下四个关于数域命题:① 是任何数域的元素;②若数域
是任何数域的元素;②若数域 中有非零元素,则
中有非零元素,则 ;③集合
;③集合 是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
①②④
解析考点:命题的真假判断与应用.
分析:根据新定义:“如果a,b∈F,则a+b,a-b,a?b∈F,并且当b≠0时, 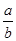 ∈F”时,我们就称F为一个数域,对①②③④进行一一验证,可以利用特殊值法进行判断;
∈F”时,我们就称F为一个数域,对①②③④进行一一验证,可以利用特殊值法进行判断;
解:①根据新定义a,b∈F,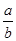 ∈F,对于a=0,可得0∈F,故①正确;
∈F,对于a=0,可得0∈F,故①正确;
②若数域F中有非零元素,F可以取实数域,可取a=2010,b=1,可得2010+1=2011∈F,故②正确;
③集合p={x|x=3k,k∈Z},p中都是3的倍数,取k=1,k=2,可得a=3,b=6,可得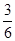 =
=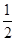 ?p,故③错误;
?p,故③错误;
④有理数是一个数域为F,对已任意a,b∈F,a+b,a-b,a?b∈F,并且当b≠0时,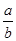 ∈F”,故④正确;
∈F”,故④正确;
故答案为:①②④;


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a | b |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省台州市高三调研考试理数 题型:填空题
当一个非空数集 满足条件“如果
满足条件“如果 则
则
 ,并且当
,并且当 时,
时, ”时,我们就称
”时,我们就称 为一个数域.以下四个关于数域命题:①
为一个数域.以下四个关于数域命题:① 是任何数域的元素;②若数域
是任何数域的元素;②若数域 中有非零元素,则
中有非零元素,则 ;③集合
;③集合 是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
当一个非空数集![]() 满足条件“如果
满足条件“如果![]() 则
则![]()
![]() ,并且当
,并且当![]() 时,
时,![]() ”时,我们就称
”时,我们就称![]() 为一个数域.以下四个关于数域命题:①
为一个数域.以下四个关于数域命题:①![]() 是任何数域的元素;②若数域
是任何数域的元素;②若数域![]() 中有非零元素,则
中有非零元素,则![]() ;③集合
;③集合![]() 是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
当一个非空数集![]() 满足条件“如果
满足条件“如果![]() 则
则![]()
![]() ,并且当
,并且当![]() 时,
时,![]() ”时,我们就称
”时,我们就称![]() 为一个数域.以下四个关于数域命题:①
为一个数域.以下四个关于数域命题:①![]() 是任何数域的元素;②若数域
是任何数域的元素;②若数域![]() 中有非零元素,则
中有非零元素,则![]() ;③集合
;③集合![]() 是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
是一个数域;④有理数集是一个数域.其中正确命题的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com