
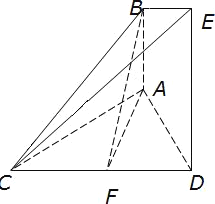
【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求直线BF和平面BCE所成角的正弦值.
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)取CE的中点G,由三角形的中位线性质证明四边形GFAB为平行四边形,得到AF∥BG,从而证明AF∥平面BCE.
(2)通过证明AF⊥CD,DE⊥AF,从而证明AF⊥平面CDE,再利用BG∥AF证明BG⊥平面CDE,进而证明平面BCE⊥平面CDE.
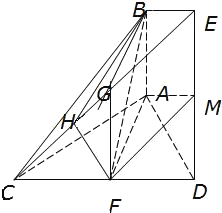
(3)在平面CDE内,过F作FH⊥CE于H,由平面BCE⊥平面CDE,得 FH⊥平面BCE,故∠FBH为BF和平面BCE所成的角,解Rt△FHB求出∠FBH的正弦值.
(1)证明:取CE的中点G,连FG、BG.
∵F为CD的中点,∴GF∥DE且![]() .
.
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.
又![]() ,∴GF=AB.
,∴GF=AB.
∴四边形GFAB为平行四边形,则AF∥BG.
∵AF平面BCE,BG平面BCE,
∴AF∥平面BCE.
(2)证明:∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.
∵DE⊥平面ACD,AF平面ACD,∴DE⊥AF.
又CD∩DE=D,故AF⊥平面CDE.
∵BG∥AF,∴BG⊥平面CDE.
∵BG平面BCE,
∴平面BCE⊥平面CDE.
(3)解:在平面CDE内,过F作FH⊥CE于H,连BH.
∵平面BCE⊥平面CDE,∴FH⊥平面BCE.
∴∠FBH为BF和平面BCE所成的角.
设AD=DE=2AB=2a,则![]() ,
,![]() ,
,
Rt△FHB中,![]() .
.
∴直线BF和平面BCE所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
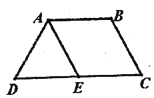
【题目】如图,等腰梯形![]() 中,
中,![]()
![]() ,
,![]() ,E为CD中点,将
,E为CD中点,将![]() 沿AE折到
沿AE折到![]() 的位置.
的位置.
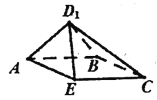
(1)证明:![]() ;
;
(2)当折叠过程中所得四棱锥![]() 体积取最大值时,求直线
体积取最大值时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() ,
,![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列,且
成等比数列,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅲ)设![]() =
=![]() +
+![]() +…+
+…+![]() ,如果对任意的正整数
,如果对任意的正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是等比数列,
是等比数列,![]() ,
,![]() ,
,![]() .判断
.判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个三口之家,共![]() 个大人,
个大人,![]() 个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐
个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐![]() 人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是_____.
人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 为椭圆
为椭圆![]() (
(![]() )和双曲线
)和双曲线![]() 的公共顶点,
的公共顶点,![]() 、
、![]() 分为双曲线和椭圆上不同于
分为双曲线和椭圆上不同于![]() 、
、![]() 的动点,且满足
的动点,且满足![]() ,设直线
,设直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)求证:点![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)求![]() 的值;
的值;
(3)若![]() 、
、![]() 分别为椭圆和双曲线的右焦点,且
分别为椭圆和双曲线的右焦点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼斯在其巨著《圆锥曲线论》中提出“在同一平面上给出三点,若其中一点到另外两点的距离之比是一个大于零且不等于1的常数,则该点轨迹是一个圆”现在,某电信公司要在甲、乙、丙三地搭建三座5G信号塔来构建一个三角形信号覆盖区域,以实现5G商用,已知甲、乙两地相距4公里,丙、甲两地距离是丙、乙两地距离的![]() 倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高山滑雪运动的曲道赛项目中,运动员从高处(起点)向下滑,在滑行中运动员要穿过多个高约0.75米,宽4至6米的旗门,规定:运动员不经过任何一个旗门,都会被判一次“失格”,滑行时间会被增加,而所用时间越少,则排名越高.已知在参加比赛的运动员中,有五位运动员在滑行过程中都有三次“失格”,其中
(1)甲在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(2)乙在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(3)丙在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(4)丁在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(5)戊在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门.
三个旗门.
根据以上信息,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这8个旗门从上至下的排列顺序共有( )种可能.
这8个旗门从上至下的排列顺序共有( )种可能.
A.6B.7C.8D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com