
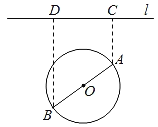
【题目】如图,一个湖的边界是圆心为![]() 的圆,湖的一侧有一条直线型公路
的圆,湖的一侧有一条直线型公路![]() ,湖上有桥
,湖上有桥![]() (
(![]() 是圆
是圆![]() 的直径).规划在公路
的直径).规划在公路![]() 上选两个点
上选两个点![]() ,
,![]() ,并修建两段直线型道路
,并修建两段直线型道路![]() ,
,![]() ,规划要求:线段
,规划要求:线段![]() ,
,![]() 上的所有点到点
上的所有点到点![]() 的距离均不小于圆
的距离均不小于圆![]() 的半径.已知点
的半径.已知点![]() ,
,![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 和
和![]() (
(![]() ,
,![]() 为垂足),测得
为垂足),测得![]() ,
,![]() ,
,![]() (单位:百米).
(单位:百米).

(1)若道路![]() 与桥
与桥![]() 垂直,求道路
垂直,求道路![]() 的长;
的长;
(2)在规划要求下,![]() 和
和![]() 中能否有一个点选在
中能否有一个点选在![]() 处?并说明理由;
处?并说明理由;
(3)在规划要求下,若道路![]() 和
和![]() 的长度均为
的长度均为![]() (单位:百米),求当
(单位:百米),求当![]() 最小时,
最小时,![]() 、
、![]() 两点间的距离.
两点间的距离.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() 中不能有点选在
中不能有点选在![]() 点,理由详见解析;(3)
点,理由详见解析;(3)![]() .
.
【解析】
(1) 设BD与圆O交于M,连接AM,以C为坐标原点,l为x轴,建立直角坐标系,利用两直线垂直的条件得直线BP的方程,求解点P的坐标,再由两点间距离公式即可求解PB的长;
(2)当QA⊥AB时,QA上的所有点到原点O的距离不小于圆的半径,设此时Q(x2,0),运用两直线垂直的条件:斜率之积为-1,求得Q的坐标,即可得到结论;
(3)设P(a,0),Q(b,0),则![]() ,
,![]() ,结合条件分析,可得b的最小值,由两点的距离公式,计算可得PQ.
,结合条件分析,可得b的最小值,由两点的距离公式,计算可得PQ.
设![]() 与圆
与圆![]() 交于
交于![]() ,连接
,连接![]() ,
,
![]() 为圆
为圆![]() 的直径,可得
的直径,可得![]() ,
,
即有![]() ,
,![]() ,
,![]() ,
,
以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴,建立直角坐标系,则
轴,建立直角坐标系,则![]() ,
,![]() ,
,![]() .
.
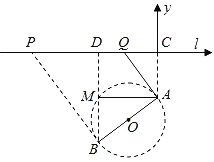
(1)设点![]() ,
,![]() ,
,
则![]() ,
,
即![]() ,
,
解得![]() ,所以
,所以![]() ,
,![]() ;
;
(2)当![]() 时,
时,![]() 上的所有点到原点
上的所有点到原点![]() 的距离不小于圆的半径,设此时
的距离不小于圆的半径,设此时![]() ,
,
则![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() ,
,
由![]() ,在此范围内,不能满足
,在此范围内,不能满足![]() ,
,![]() 上所有点到
上所有点到![]() 的距离不小于圆的半径,
的距离不小于圆的半径,
所以![]() ,
,![]() 中不能有点选在
中不能有点选在![]() 点;
点;
(3)设![]() ,
,![]() ,由(1)(2)可得
,由(1)(2)可得![]() ,
,![]() ,
,
由两点的距离公式可得![]() ,
,
当且仅当![]() 时,
时,![]() 取得最小值15,
取得最小值15,
又![]() ,则
,则![]() ,当
,当![]() 最小时,
最小时,![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】有两种理财产品![]() 和
和![]() ,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
注:![]() ,
,![]()
(1)若甲、乙两人分别选择了产品![]() 投资,一年后他们中至少有一人获利的概率大于
投资,一年后他们中至少有一人获利的概率大于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若丙要将20万元人民币投资其中一种产品,以一年后的投资收益的期望值为决策依据,则丙选择哪种产品投资较为理想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行六面体ABCD﹣A1B1C1D1中,所有棱长均为2,∠AA1D1=∠AA1B1=60°,∠D1A1B1=90°.
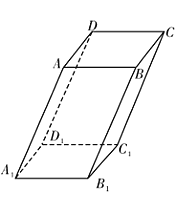
(1)求证:A1C⊥B1D1;
(2)求对角线AC1的长;
(3)求二面角C1﹣AB1﹣D1的平面角的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词,寻文化基因,品生活之美”为宗旨.每一期的比赛包含以下环节:“个人追逐赛”、“攻擂资格争夺赛”和“擂主争霸赛”,其中“擂主争霸赛”由“攻擂资格争夺赛”获胜者与上一场擂主进行比拼.“擂主争霸赛”共有九道抢答题,抢到并答对者得一分,答错则对方得一分,率先获得五分者即为该场擂主.在《中国诗词大会》的某一期节目中,若进行“擂主争霸赛”的甲乙两位选手每道抢答题得到一分的概率都是为0.5,则抢答完七道题后甲成为擂主的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线
为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() .若直线
.若直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com