
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为![]() ,求△AOB面积的最大值,并求此时直线l的方程.
,求△AOB面积的最大值,并求此时直线l的方程.
科目:高中数学 来源: 题型:
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如表所示:
(天)之间的关系如表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |

(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附: 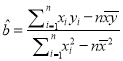 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数y=f(x),x∈D(定义域),若存在常数C,对于任意x1∈D,存在唯一的x2∈D,使得 ![]() =C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
=C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
A.![]()
B.![]()
C.![]()
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆E的左右顶点分别为A、B,左右焦点分别为![]() 、
、![]() ,
,![]() ,直线
,直线![]() 交椭圆于C、D两点,与线段
交椭圆于C、D两点,与线段![]() 及椭圆短轴分别交于
及椭圆短轴分别交于![]() 两点(
两点(![]() 不重合),且
不重合),且![]() .
.

(Ⅰ)求椭圆E的离心率;
(Ⅱ)若![]() ,设直线
,设直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“足寒伤心,民寒伤国”,精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对石山区乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量![]() 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费![]() 万元之间的函数关系为
万元之间的函数关系为![]() (其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本
(其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本![]() 万元(不包含推广促销费用),若加工后的每件成品的销售价格定为
万元(不包含推广促销费用),若加工后的每件成品的销售价格定为![]() 元/件.
元/件.
(1)试将该批产品的利润![]() 万元表示为推广促销费
万元表示为推广促销费![]() 万元的函数;(利润
万元的函数;(利润![]() 销售额
销售额![]() 成本
成本![]() 推广促销费)
推广促销费)
(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 从
从![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() ,
, ![]() ,
, ![]() 三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com