
【题目】如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为16,20,则输出的a=( ) 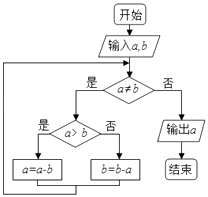
A.0
B.2
C.4
D.14
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】将函数f(x)=cos2x图象向左平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象,若函数g(x)在区间[﹣
)个单位后得到函数g(x)的图象,若函数g(x)在区间[﹣ ![]() ,
, ![]() ]上单调递减,且函数g(x)的最大负零点在区间(﹣
]上单调递减,且函数g(x)的最大负零点在区间(﹣ ![]() ,0)上,则φ的取值范围是( )
,0)上,则φ的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1 , 且AA1=AB=2. 
(1)求证:AB⊥BC;
(2)若直线AC与平面A1BC所成的角为 ![]() ,求锐二面角A﹣A1C﹣B的大小.
,求锐二面角A﹣A1C﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinA,
=(sinA, ![]() )与
)与 ![]() =(3,sinA+
=(3,sinA+ ![]() )共线,其中A是△ABC的内角.
)共线,其中A是△ABC的内角.
(1)求角A的大小;
(2)若BC=2,求△ABC面积S的最大值,并判断S取得最大值时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由半圆x2+y2=r2(y≤0,r>0)和部分抛物线y=a(x2﹣1)(y≥0,a>0)合成的曲线C称为“羽毛球形线”,曲线C与x轴有A、B两个焦点,且经过点(2.3). 
(1)求a、r的值;
(2)设N(0,2),M为曲线C上的动点,求|MN|的最小值;
(3)过A且斜率为k的直线l与“羽毛球形线”相交于P,A,Q三点,问是否存在实数k,使得∠QBA=∠PBA?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com