
【题目】如图,棱长为1的正方体![]() 中,
中,![]() 为线段
为线段![]() 的动点,则下列4个命题中正确的有( )个
的动点,则下列4个命题中正确的有( )个
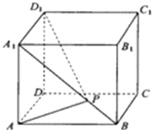
(1)![]() (2)平面
(2)平面![]() 平面
平面![]()
(3)![]() 的最大值为
的最大值为![]() (4)
(4)![]() 的最小值为
的最小值为![]()
A.1B.2C.3D.4
【答案】C
【解析】
分别连接![]() ,
,![]() ,作出图形后逐一
,作出图形后逐一
对于(1),利用线面垂直的判定定理可证![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,故(1)正确;
,故(1)正确;
对于(2),![]() 平面
平面![]() ,而平面
,而平面![]() ,就是平面
,就是平面![]() ,
,
故平面![]() 平面
平面![]() ,从而可判定(2)正确;
,从而可判定(2)正确;
对于(3),当![]() 时,
时,![]() 为钝角,故可判断(3)错误;
为钝角,故可判断(3)错误;
对于(4),将面![]() 与面
与面![]() 沿
沿![]() 展成平面图形,线段
展成平面图形,线段![]() 即为
即为![]() 的最小值,通过解三角形
的最小值,通过解三角形![]() 可求得
可求得![]() ,可判断(4)正确.
,可判断(4)正确.
分别连接![]() ,
,![]() ,如图:
,如图:
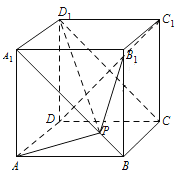
对于(1),∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,正确;
,正确;
对于(2),∵平面![]() 即为平面
即为平面![]() ,平面
,平面![]() 即为平面
即为平面![]() ,
,
且![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,正确;
,正确;
对于(3),在![]() 中,由余弦定理可知,当
中,由余弦定理可知,当![]() 时,
时,![]() 为钝角,错误;
为钝角,错误;
对于(4),将面![]() 与面
与面![]() 沿
沿![]() 展成平面图形,线段
展成平面图形,线段![]() 即为
即为![]() 的最小值,
的最小值,
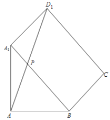
在![]() 中,利用余弦定理解三角形得
中,利用余弦定理解三角形得![]() ,正确.
,正确.
故选:C.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是曲线段
是曲线段![]() :
:![]() (
(![]() 是参数,
是参数,![]() )的左、右端点,
)的左、右端点,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
(1)建立适当的极坐标系,写出点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
,部分对应值如表,![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的结论正确的是( )
的结论正确的是( )
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
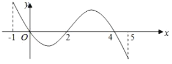
A.函数![]() 的极大值点有2个
的极大值点有2个
B.函数![]() 在
在![]() 上是减函数
上是减函数
C.若![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4
的最大值为4
D.当![]() 时,函数
时,函数![]() 有4个零点
有4个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点![]() ,且离心率为
,且离心率为![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过原点的直线![]() 与椭圆C交于P、Q两点,且在直线
与椭圆C交于P、Q两点,且在直线![]() 上存在点M,使得
上存在点M,使得![]() 为等边三角形,求直线
为等边三角形,求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为![]() .
.
(1)问该厂至少有多少名维修工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不小于![]() ?
?
(2)已知1名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,能使该厂产生5万元的利润,否则将不产生利润.若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com