
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 。
。
(1)求曲线![]() 的极坐标方程和直线l的直角坐标方程;
的极坐标方程和直线l的直角坐标方程;
(2)设直线l与曲线![]() 交于不同的两点A,B,点M为抛物线
交于不同的两点A,B,点M为抛物线![]() 的焦点,求
的焦点,求![]() 的值。
的值。
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数具有性质
,则称函数具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并证明:①
,并证明:①![]() (
(![]() );②
);②![]() ;
;
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() (
(![]() ,
,![]() ),
),
①求证:对任意![]() ,有
,有![]() ;
;
②是否对任意![]() ,均有
,均有![]() ?若有,给出证明,若没有,给出反例.
?若有,给出证明,若没有,给出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组在研究性学习中,对昼夜温差大小与绿豆种子一天内出芽数之间的关系进行研究.该小组在4月份记录了1日至6日每天昼夜最高、最低温度(如图1),以及浸泡的100颗绿豆种子当天内的出芽数(如图2).
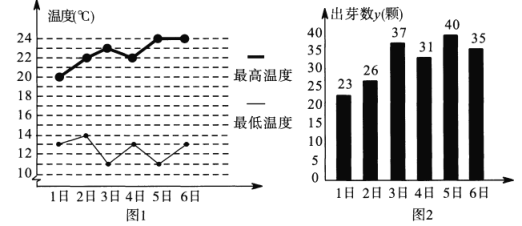
根据上述数据作出散点图,可知绿豆种子出芽数![]() (颗)和温差
(颗)和温差![]() (
(![]() )具有线性相关关系.
)具有线性相关关系.
(1)求绿豆种子出芽数![]() (颗)关于温差
(颗)关于温差![]() (
(![]() )的回归方程
)的回归方程![]() ;
;
(2)假如4月1日至7日的日温差的平均值为11![]() ,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
,估计4月7日浸泡的10000颗绿豆种子一天内的出芽数.
附: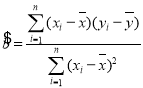
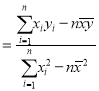 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为4.
,短轴长为4.
(1)求椭圆C的标准方程.
(2)设直线l过点(2,0)且与椭圆C相交于不同的两点A、B,直线![]() 与x轴交于点D,E是直线
与x轴交于点D,E是直线![]() 上异于D的任意一点,当
上异于D的任意一点,当![]() 时,直线BE是否恒过x轴上的定点?若过,求出定点坐标,若不过,请说明理由。
时,直线BE是否恒过x轴上的定点?若过,求出定点坐标,若不过,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乐园按时段收费,收费标准为:每玩一次不超过![]() 小时收费10元,超过
小时收费10元,超过![]() 小时的部分每小时收费
小时的部分每小时收费![]() 元(不足
元(不足![]() 小时的部分按
小时的部分按![]() 小时计算).现有甲、乙二人参与但都不超过
小时计算).现有甲、乙二人参与但都不超过![]() 小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
小时,甲、乙二人在每个时段离场是等可能的。为吸引顾客,每个顾客可以参加一次抽奖活动。
(1) 用![]() 表示甲乙玩都不超过
表示甲乙玩都不超过![]() 小时的付费情况,求甲、乙二人付费之和为44元的概率;
小时的付费情况,求甲、乙二人付费之和为44元的概率;
(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数![]() ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
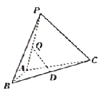
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕边AB翻转至
绕边AB翻转至![]() ,使面
,使面![]() 面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
面ABC,D是BC的中点,设Q是线段PA上的动点,则当PC与DQ所成角取得最小值时,线段AQ的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com