
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点
的焦点
(1)求椭圆![]() 的方程;
的方程;
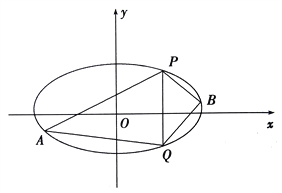
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点, ![]() ,
, ![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.①若直线
两侧的动点.①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() ,
, ![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析: (1)由椭圆的离心率及短轴端点坐标求出![]() ,得到椭圆方程; (2)①设
,得到椭圆方程; (2)①设![]() 设直线AB方程为
设直线AB方程为![]() ,联立直线与椭圆方程,消去
,联立直线与椭圆方程,消去![]() ,得到一个关于
,得到一个关于![]() 的二次方程,求出
的二次方程,求出![]() ,再求出
,再求出![]() ,代入三角形面积公式,求出最大值; ②由
,代入三角形面积公式,求出最大值; ②由![]() 得到直线
得到直线![]() 斜率之和为0,设直线
斜率之和为0,设直线![]() 斜率为
斜率为![]() ,则直线
,则直线![]() 斜率为
斜率为![]() ,直线
,直线![]() 方程为
方程为![]() ,代入椭圆方程中,求出
,代入椭圆方程中,求出![]() 的表达式,同理求出
的表达式,同理求出![]() 的表达式,再求出
的表达式,再求出![]() 的值,代入直线
的值,代入直线![]() 的斜率计算公式中,结果为定值.
的斜率计算公式中,结果为定值.
试题解析:(1)![]() ∴
∴![]()
∴![]()
![]() 又
又 ![]()
∴![]()
![]() ∴ 椭圆方程为
∴ 椭圆方程为![]()
(2)①设 ![]() ,
, ![]()
设![]() 方程
方程 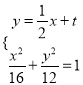 代入化简
代入化简 ![]()
![]() ,
, ![]()
![]() 又
又![]() 、
、![]()
![]()
当![]() 时,
时, ![]() 最大为
最大为![]()
②当![]() 时,
时, ![]() 、
、![]() 斜率之和为
斜率之和为![]() .
.
设![]() 斜率为
斜率为![]() ,则
,则![]() 斜率为
斜率为![]()
设 代入化简 同理 ∴ 直线 点睛:本题主要考查了椭圆的标准方程及性质,直线与椭圆相交问题,一元二次方程根与系数关系,斜率的计算公式,考查了推理与计算能力, 属于难题.![]() 方程
方程![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() 的斜率为定值
的斜率为定值![]()


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】某厂生产的产品在出厂前都要做质量检测,每件一等品都能通过检测,每件二等品通过检测的概率为![]() .现有
.现有![]() 件产品,其中
件产品,其中![]() 件是一等品,
件是一等品, ![]() 件是二等品.
件是二等品.
(Ⅰ)随机选取![]() 件产品,设至少有一件通过检测为事件
件产品,设至少有一件通过检测为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(Ⅱ)随机选取![]() 件产品,其中一等品的件数记为
件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位职工义务献血,在体检合格的人中, ![]() 型血的共有28人,
型血的共有28人, ![]() 型血的共有7人,
型血的共有7人, ![]() 型血的共有9人,
型血的共有9人, ![]() 型血的有3人.
型血的有3人.
(1)从中任选1人去献血,有多少种不同的选法?
(2)从四种血型的人中各选1人去献血,有多少种不同的选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨,现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天数![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosωx,sinωx),
=(cosωx,sinωx), ![]() =(cosωx,
=(cosωx, ![]() cosωx),其中ω>0,设函数f(x)=
cosωx),其中ω>0,设函数f(x)= ![]()
![]() .
.
(1)若函数f(x)的最小正周期是π,求函数f(x)的单调递增区间;
(2)若函数f(x)的图象的一个对称中心的横坐标为 ![]() ,求ω的最小值.
,求ω的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com