
【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中.随机选
小块地中.随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(![]() )假设
)假设![]() ,求第一大块地都种植品种甲的概率.
,求第一大块地都种植品种甲的概率.
(![]() )试验时每大块地分成
)试验时每大块地分成![]() 小块.即
小块.即![]() ,试验结束后得到品种甲和品种乙在各个小块地上的每公顷产量(单位
,试验结束后得到品种甲和品种乙在各个小块地上的每公顷产量(单位![]() )如下表:
)如下表:
品种甲 |
|
|
|
|
|
品种乙 |
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由古典概型的公式得到从![]() 小块地中任选
小块地中任选![]() 小块地种植品种甲的基本事件有6件,第一大块地都种品种甲件数1件,故得到概率为
小块地种植品种甲的基本事件有6件,第一大块地都种品种甲件数1件,故得到概率为![]() ;(2)根据图标得到相应的平均数和方差,可分析出结果.
;(2)根据图标得到相应的平均数和方差,可分析出结果.
解析:
(![]() )设第一大块地中的两小块地编号为
)设第一大块地中的两小块地编号为![]() ,
, ![]() ,
,
第二大块地中的两小块地编号为![]() ,
, ![]() ,
,
令事件![]() “第一大块地都种品种甲”,从
“第一大块地都种品种甲”,从![]() 小块地中任选
小块地中任选![]() 小块地种植品种甲的基本事件有:
小块地种植品种甲的基本事件有:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共
共![]() 个,
个,
而事件![]() 包含
包含![]() 个基本事件:
个基本事件: ![]() .
.
故![]() .
.
(![]() )品种甲的每公顷产量的样本平均数和方差分别为:
)品种甲的每公顷产量的样本平均数和方差分别为:
![]() ,
,
![]() ,
,
品种乙的每公顷产量的样本平均数和方差分别为:
![]() ,
,
![]() ,
,
由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差相同,故应选择种植品种乙.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】采用系统抽样方法从![]() 人中抽取
人中抽取![]() 人做问卷调查,为此将他们随机编号为
人做问卷调查,为此将他们随机编号为![]() ,
,![]() ,
,![]() ,
,![]() ,分组后某组抽到的号码为41.抽到的
,分组后某组抽到的号码为41.抽到的![]() 人中,编号落入区间
人中,编号落入区间![]() 的人数为( )
的人数为( )
A. 10 B. ![]() C. 12 D. 13
C. 12 D. 13
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轮船在海上航行时,需要借助无线电导航确认自己所在的位置,以把握航向.现有![]() 、
、![]() 、
、![]() 三个无线电发射台,其中
三个无线电发射台,其中![]() 在陆地上,
在陆地上,![]() 在海上,
在海上,![]() 在某国海岸线上,(该国这段海岸线可以近似地看作直线的一部分),如下图.已知
在某国海岸线上,(该国这段海岸线可以近似地看作直线的一部分),如下图.已知![]() 、
、![]() 两点距离10千米,
两点距离10千米,![]() 是
是![]() 的中点,海岸线与直线
的中点,海岸线与直线![]() 的夹角为
的夹角为![]() .为保证安全,轮船的航路始终要满足:接收到
.为保证安全,轮船的航路始终要满足:接收到![]() 点的信号比接收到
点的信号比接收到![]() 点的信号晚
点的信号晚![]() 秒.(注:无线电信号每秒传播
秒.(注:无线电信号每秒传播![]() 千米).在某时刻,测得轮船距离
千米).在某时刻,测得轮船距离![]() 点距离为4千米.
点距离为4千米.

(1)以点![]() 为原点,直线
为原点,直线![]() 为
为![]() 轴建立平面直角坐标系(如图),求出该时刻轮船的位置;
轴建立平面直角坐标系(如图),求出该时刻轮船的位置;
(2)根据经验,船只在距离海岸线1.5千米以内的海域航行时,有搁浅的风险.如果轮船保持目前的航路不变,那么是否有搁浅风险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是各项均为正数的数列
是各项均为正数的数列![]() 的前
的前![]() 项和,且
项和,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,且数列
,且数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() 对任意正整数
对任意正整数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设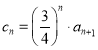 ,问:是否存在正整数
,问:是否存在正整数![]() ,使得
,使得![]() 对一切正整数
对一切正整数![]() 恒成立?若存在,请求出实数
恒成立?若存在,请求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司引进了一套无人智能配货系统,购买系统的费用为80万元,维持系统正常运行的费用包括保养费和维修费两部分,每年的保养费用为1万元.该系统的维修费为:第一年![]() 万元,第二年
万元,第二年![]() 万元,第三年2万元,…,依等差数列逐年递增.
万元,第三年2万元,…,依等差数列逐年递增.
(1)求该系统使用n年的总费用![]() (包括购买设备的费用);
(包括购买设备的费用);
(2)求该系统使用多少年报废,使年平均费用最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com