
【题目】已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.
(1)求函数f(x)(x∈R)的解析式;
(2)现已画出函数f(x)在y轴左侧的图象,如图所示,请补全完整函数f(x)的图象;
(3)求使f(x)>0的实数x的取值集合.
【答案】
(1)解:设x>0,则﹣x<0,
∴f(﹣x)=(﹣x)2+2×(﹣x)=x2﹣2x,
∵函数f(x)是定义在R上的奇函数,
∴f(x)=﹣f(﹣x)=﹣x2+2x(x>0),
∴ ![]()
(2)解:函数的图象如图所示:
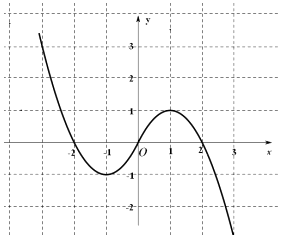
(3)解:方程f(x)=0的根是x1=﹣2,x2=0,x3=2,
由函数的图象可知不等式f(x)>0的解集为{x|x<﹣2或0<x<2}
【解析】(1)根据f(-x)=-f(x)求出当x![]() 0时函数f(x)的解析式;(2)根据奇函数图象的对称性;(3)结合(2)的图象即可求解.
0时函数f(x)的解析式;(2)根据奇函数图象的对称性;(3)结合(2)的图象即可求解.
【考点精析】认真审题,首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值).


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. 
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四名选手 A、B、C、D 参加射击、抛球、走独木桥三项比赛,每个选手在各项比赛中获得合格、不合格机会相等,比赛结束,评委们会根据选手表现给每位选手评定比赛成绩,根据比赛成绩,对前两名进行奖励.
(1)选手 D 至少获得两个合格的概率;
(2)选手 C、D 只有一人得到奖励的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n∈R,若直线l:mx+ny﹣1=0与x轴相交于点A,与y轴相交于点B,且l与圆x2+y2=4相交所得弦的长为2,O为坐标原点,则△AOB面积的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面区域  恰好被面积最小的圆C:(x﹣a)2+(y﹣b)2=r2及其内部所覆盖.
恰好被面积最小的圆C:(x﹣a)2+(y﹣b)2=r2及其内部所覆盖.
(1)试求圆C的方程.
(2)若斜率为1的直线l与圆C交于不同两点A,B满足CA⊥CB,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax﹣1)(x+b),如果不等式f(x)>0的解集是(﹣1,3),则不等式f(﹣x)<0的解集是( )
A.(﹣∞,﹣1)∪(3,+∞)
B.(﹣3,1)
C.(﹣∞,﹣3)∪(1,+∞)
D.(﹣1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,AA1 , AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com