
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对一切![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:对一切![]() ,都有
,都有![]() 成立.
成立.
【答案】(1)递增区间是![]() ,递减区间是
,递减区间是![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】试题分析:(1)求出函数的导数,解关于导数的不等式,即可求解函数的单调区间;
(2)问题可化为![]() 对一切
对一切![]() 恒成立,令
恒成立,令![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() 的最小值,从而求出
的最小值,从而求出![]() 的取值范围即可;
的取值范围即可;
(3)问题等价于![]() ,即证
,即证![]() ,令
,令![]() ,根据函数的单调性即可作出证明.
,根据函数的单调性即可作出证明.
试题解析:
(1)![]() ,得
,得![]() 由
由![]() ,得
,得![]()
∴![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]()
(2)对一切![]() ,
, ![]() 恒成立,
恒成立,
可化为![]() 对一切
对一切![]() 恒成立.
恒成立.
令![]() ,
, ![]()
![]() ,
, ![]()
当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 递减
递减
当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 递增,∴
递增,∴![]() ,
,
∴![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]()
(3)证明: ![]() 等价于
等价于![]() ,即证
,即证![]()
由(1)知![]() ,(当
,(当![]() 时取等号)
时取等号)
令![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 递减,在
递减,在![]() 递增
递增
∴![]() (当
(当![]() 时取等号)∴
时取等号)∴![]() 对一切
对一切![]() 都成立
都成立
则对一切![]() ,都有
,都有![]() 成立.
成立.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知集合M={1,2,3},N={1,2,3,4},定义函数f:M→N.若点A(1,f(1))、B(2,f(2))、C(3,f(3)),△ABC的外接圆圆心为D,且 ![]() ,则满足条件的函数f(x)有( )
,则满足条件的函数f(x)有( )
A.6个
B.10个
C.12个
D.16个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,矩形ABCD的边AB=m,BC=4,PA⊥平面ABCD,PA=3,现有数据:
① ![]() ;②m=3;③m=4;④
;②m=3;③m=4;④ ![]() .若在BC边上存在点Q(Q不在端点B、C处),使PQ⊥QD,则m可以取( )
.若在BC边上存在点Q(Q不在端点B、C处),使PQ⊥QD,则m可以取( )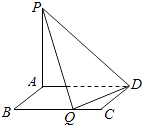
A.①②
B.①②③
C.②④
D.①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布图如图所示,下表是年龄的频率分布表.
,得到的频率分布图如图所示,下表是年龄的频率分布表.
![]()

(1)现要从年龄较小的第![]() 组中用分层抽样的方法抽取6人,则年龄第
组中用分层抽样的方法抽取6人,则年龄第![]() 组人数分别是多少?
组人数分别是多少?
(2)在(1)的条件下,从这6中随机抽取2参加社区宣传交流活动,求恰有2人在第3组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数m取什么数值时,复数z=m2﹣1+(m2﹣m﹣2)i分别是:
(1)实数?
(2)虚数?
(3)纯虚数?
(4)表示复数z的点在复平面的第四象限?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com