
【题目】已知函数 ![]() .
.
(1)判断并证明函数f(x)在其定义域上的奇偶性;
(2)证明函数f(x)在(1,+∞)上是增函数.
【答案】
(1)解:∵函数 ![]() .
.
∴a+1=2,∴a=1,
∴ ![]() ,
,
∴f(x)的定义域{x|x≠0}关于原点对称,
∴ ![]() ,
,
∴f(x)是定义域上的奇函数
(2)证明:任取x1,x2∈(1,+∞),且x1<x2,
则 ![]() ,
,
∵x1<x2,∴x1﹣x2<0,
又x1,x2∈(1,+∞),
∴x1x2>1x1x2﹣1>0,
∴f(x1)﹣f(x2)<0,
∴函数f(x)在(1,+∞)上是增函数
【解析】(1)由f(1)=2求出a的值,得f(x)的解析式,从而判定f(x)的奇偶性.(2)用单调性定义证明f(x)在(1,+∞)上的增减性.
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较),还要掌握函数的奇偶性(偶函数的图象关于y轴对称;奇函数的图象关于原点对称)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】在某校科普知识竞赛前的模拟测试中,得到甲、乙两名学生的6次模拟测试成绩(百分制)的茎叶图.
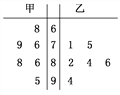
(I)若从甲、乙两名学生中选择一人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(II)若从甲的6次模拟测试成绩中随机选择2个,记选出的成绩中超过87分的个数为随机变量ξ,求ξ的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的值满足f(x)<0,对任意实数x,y都有f(xy)=f(x)f(y),且f(﹣1)=1,f(27)=9,当0<x<1时,f(x)∈(0,1).
(1)求f(1)的值,判断f(x)的奇偶性并证明;
(2)判断f(x)在(0,+∞)上的单调性,并给出证明;
(3)若a≥0且f(a+1)≤ ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ![]() ,其中
,其中 ![]() )
)
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽 ![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量 ![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.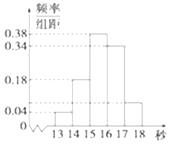
(1)设m,n表示样本中两个学生的百米测试成绩,已知m,n∈[13,14)∪[17,18],求事件“|m-n|>2”的概率;
(2)根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否在犯错误的概率不超过0.01的前提下认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附: 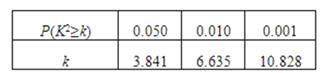
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考公式及数据: 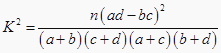
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com